题目内容
已知
=(x+
,y),
=(x-
,y),且|
|+|
|=6,则|2x-3y-12|的最大值为 .
| OA |
| 5 |
| OB |
| 5 |
| OA |
| OB |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:运用向量模的公式,结合椭圆的定义,求得点(x,y)的轨迹方程,求出椭圆的参数方程,运用两角差的正弦公式,计算即可得到最大值.
解答:
解:由于
=(x+
,y),
=(x-
,y),
则|
|+|
|=6,
即为
+
=6,
表示点(x,y)与点E(-
,0)和F(
,0)的距离之和为6,
由椭圆的定义,由6>2
,可得点(x,y)在以E,F为焦点,长轴长为6的椭圆上,
即有a=3,c=
,b=2,
方程为
+
=1,
可令x=3cosα,y=2sinα(0≤α<2π).
则|2x-3y-12|=|6cosα-6sinα-12|=|6
sin(α-
)-12|=12-6
sin(α-
),
当sin(α-
)=-1即α=
时,取得最大值12+6
.
故答案为:12+6
.
| OA |
| 5 |
| OB |
| 5 |
则|
| OA |
| OB |
即为
(x+
|
(x-
|
表示点(x,y)与点E(-
| 5 |
| 5 |
由椭圆的定义,由6>2
| 5 |
即有a=3,c=
| 5 |
方程为
| x2 |
| 9 |
| y2 |
| 4 |
可令x=3cosα,y=2sinα(0≤α<2π).
则|2x-3y-12|=|6cosα-6sinα-12|=|6
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
当sin(α-
| π |
| 4 |
| 7π |
| 4 |
| 2 |
故答案为:12+6
| 2 |
点评:本题考查椭圆的定义和方程,考查椭圆的参数方程的运用,考查三角函数的化简和求值,考察运算能力,属于中档题.

练习册系列答案
相关题目
直线l的方向向量
=(-1,1,1),平面π的法向量为
=(2,x2+x,-x),若直线l∥平面π,则实数x的值为( )
| s |
| n |
| A、-2 | ||
B、-
| ||
C、
| ||
D、±
|
函数y=
的单调递增区间是( )
| lnx |
| x |
A、(0,
| ||
B、(
| ||
| C、(0,e) | ||
| D、(e,+∞) |
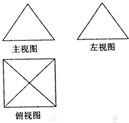 一个几何体的三视图如图所示,其中主(正)视图是边长为2的正三角形,俯视图是正方形,那么该几何体的左(侧)视图的面积是( )
一个几何体的三视图如图所示,其中主(正)视图是边长为2的正三角形,俯视图是正方形,那么该几何体的左(侧)视图的面积是( )
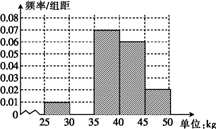 某养猪厂计划将重量为25kg到50kg的10000头猪向外出售,现从中随机抽取了100头猪进行称重,已知这些猪的重量的频率分布表及不完整的频率分布直方图(如图).
某养猪厂计划将重量为25kg到50kg的10000头猪向外出售,现从中随机抽取了100头猪进行称重,已知这些猪的重量的频率分布表及不完整的频率分布直方图(如图).