题目内容

3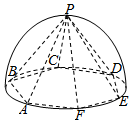．如图，半径为2的半球内有一内接正六棱锥P-ABCDEF（底面正六边形ABCDEF的中心为球心）．求：正六棱锥P-ABCDEF的体积和侧面积．

分析 正六棱锥P-ABCDEF的底面的外接圆是球的一个大圆，求出正六边形的边长，求出侧面斜高，即可求出正六棱锥的体积、侧面积．

解答 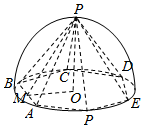解：设底面中心为O，AB中点为M，连结PO、OM、PM、AO，则PO⊥OM，OM⊥AF，PM⊥AF，
∵OA=OP=2，∴OM=$\sqrt{3}$，
∴S底=6×$\frac{1}{2}$×2×$\sqrt{3}$=6$\sqrt{3}$．
∴V=$\frac{1}{3}$×6$\sqrt{3}$×2=4$\sqrt{3}$．…6分
∵PM=$\sqrt{4+3}$=$\sqrt{7}$．…8分
∴S侧=6×$\frac{1}{2}$×2×$\sqrt{7}$=6$\sqrt{7}$．…12分．

点评 本题是基础题，考查空间想象能力，计算能力，能够得到底面是大圆，求出斜高，本题即可解决，强化几何体的研究，是解好立体几何问题的关键．

练习册系列答案
相关题目
13．若f（cosx）=3-sin2x，则f（sinx）=（　　）
A．3-cos2xB．3-sin2xC．3+cos2xD．3+sin2x
14．复数z满足（$\overline z$-3）（2-i）=5（i为虚数单位），则z为（　　）
A．-2+iB．2-iC．5+iD．5-i
11．已知向量$\overrightarrow{a}$=（1，1，0），则与$\overrightarrow{a}$共线的单位向量$\overrightarrow{e}$=（　　）
A．（$\frac{\sqrt{2}}{2}$，-$\frac{\sqrt{2}}{2}$，0）B．（0，1，0）C．（$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{2}}{2}$，0）D．（1，1，1）
18．某科技创新大赛设有一、二、三等奖（参与活动的都有奖）且相应奖项获奖的概率是以a为首项，2为公比的等比数列，相应的奖金分别是以7000元、5600元、4200元，则参加此次大赛获得奖金的期望是5000元．
8．（Ⅰ）化简$\frac{sin（2π-α）tan（α+π）tan（-α）}{cos（π-α）tan（3π-α）}$．
（Ⅱ）计算$cos\frac{25π}{6}+cos\frac{25π}{3}+tan（{-\frac{25π}{4}}）+sin\frac{5π}{6}$．
15．某高校从参加自主招生考试的学生中随机抽取容量为100的学生成绩样本，得到频率分布表如表：
组号分组频数频率
第一组[235，240）240.24
第二组[240，245）16②
第三组[245，250）①0.3
第四组[250，255）200.20
第五组[255，260]100.10
合              计1001.00
（1）上表中①②位置的数据分别是多少？
（2）为了更多了解第三组、第四组、第五组的学生情况，该高校决定在这三个组中用分层抽样法抽取6名学生进行考察，这三个组参加考核的人数分别是多少？
12．直线y=x-1的倾斜角为45度．
13．已知△ABC的外接圆半径为1，圆心为O，且$\overrightarrow{OA}$$+\overrightarrow{OB}$$+\sqrt{2}$$\overrightarrow{OC}$=0，则△ABC的面积为（　　）
A．1+$\sqrt{2}$B．$\frac{1}{2}$+$\sqrt{2}$C．1+$\frac{\sqrt{2}}{2}$D．$\frac{1}{2}+\frac{\sqrt{2}}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网