题目内容
13.已知△ABC的外接圆半径为1,圆心为O,且$\overrightarrow{OA}$$+\overrightarrow{OB}$$+\sqrt{2}$$\overrightarrow{OC}$=0,则△ABC的面积为( )| A. | 1+$\sqrt{2}$ | B. | $\frac{1}{2}$+$\sqrt{2}$ | C. | 1+$\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}+\frac{\sqrt{2}}{2}$ |
分析 由条件得$\overrightarrow{OA}+\overrightarrow{OB}=-\sqrt{2}\overrightarrow{OC}$.两边平方计算$\overrightarrow{OA}•\overrightarrow{OB}$,得出∠AOB.从而得出∠AOC,∠BOC,分别计算三个小三角形的面积即可.
解答 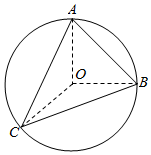 解:∵△ABC的外接圆半径为1,圆心为O,
解:∵△ABC的外接圆半径为1,圆心为O,
∴OA=OB=OC=1.
∵$\overrightarrow{OA}$$+\overrightarrow{OB}$$+\sqrt{2}$$\overrightarrow{OC}$=$\overrightarrow{0}$,
∴$\overrightarrow{OA}+\overrightarrow{OB}=-\sqrt{2}\overrightarrow{OC}$.
∴${\overrightarrow{OA}}^{2}+{\overrightarrow{OB}}^{2}+2\overrightarrow{OA}•\overrightarrow{OB}=2{\overrightarrow{OC}}^{2}$,即1+1+2$\overrightarrow{OA}•\overrightarrow{OB}$=2.
∴$\overrightarrow{OA}•\overrightarrow{OB}=0$.
∴$\overrightarrow{OA}⊥\overrightarrow{OB}$,即∠AOB=90°,
∴∠AOC=∠BOC=135°,
∴S△ABC=S△AOB+S△AOC+S△BOC=$\frac{1}{2}×1×1×sin90°$+$\frac{1}{2}×1×1×sin135°$+$\frac{1}{2}×1×1×sin135°$=$\frac{1}{2}+\frac{\sqrt{2}}{2}$.
故选D.
点评 本题考查了平面向量在几何中的应用,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 相交 | B. | 内切 | C. | 相离 | D. | 外切 |
| A. | $\frac{\sqrt{3}}{3}$R | B. | $\frac{1}{3}$πR | C. | $\frac{1}{2}$πR | D. | $\frac{2}{3}$πR |
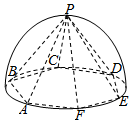 如图,半径为2的半球内有一内接正六棱锥P-ABCDEF(底面正六边形ABCDEF的中心为球心).求:正六棱锥P-ABCDEF的体积和侧面积.
如图,半径为2的半球内有一内接正六棱锥P-ABCDEF(底面正六边形ABCDEF的中心为球心).求:正六棱锥P-ABCDEF的体积和侧面积.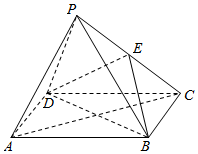 如图,四棱锥P-ABCD中,底面ABCD是边长等于2的正方形,其他四个侧面都是边长等于$\sqrt{5}$的等腰三角形,点E是PC中点.
如图,四棱锥P-ABCD中,底面ABCD是边长等于2的正方形,其他四个侧面都是边长等于$\sqrt{5}$的等腰三角形,点E是PC中点.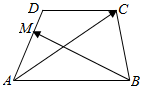 如图,在梯形ABCD中,AB∥CD,AB=4,AD=3,CD=2,$\overrightarrow{AM}$=2$\overrightarrow{MD}$,若$\overrightarrow{AC}$•$\overrightarrow{BM}$=-3,则$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\frac{3}{2}$.
如图,在梯形ABCD中,AB∥CD,AB=4,AD=3,CD=2,$\overrightarrow{AM}$=2$\overrightarrow{MD}$,若$\overrightarrow{AC}$•$\overrightarrow{BM}$=-3,则$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\frac{3}{2}$.