若椭圆$\frac{{y}^{2}}{100}+\frac{{x}^{2}}{36}$=1上一点P到焦点F1的距离等于6.点P到另一个焦点F2的距离是( )A．20B．14C．4D．24 题目和参考答案——青夏教育精英家教网—

题目内容

13．若椭圆$\frac{{y}^{2}}{100}+\frac{{x}^{2}}{36}$=1上一点P到焦点F₁的距离等于6，点P到另一个焦点F₂的距离是（　　）

A．

B．

C．

D．

分析由题意可知：椭圆$\frac{{y}^{2}}{100}+\frac{{x}^{2}}{36}$=1焦点在x轴上，a=10，b=6，c=8，丨PF₁丨=6，由由椭圆的性质可知：丨PF₁丨+丨PF₂丨=2a=20，因此丨PF₂丨=14，即点P到另一个焦点F₂的距离14．

解答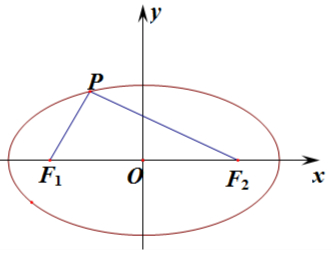解：由椭圆$\frac{{y}^{2}}{100}+\frac{{x}^{2}}{36}$=1焦点在x轴上，a=10，b=6，c=8，
P到焦点F₁的距离等于6，即丨PF₁丨=6，
由椭圆的性质可知：丨PF₁丨+丨PF₂丨=2a=20，
∴丨PF₂丨=14，
∴点P到另一个焦点F₂的距离14，
故选：B．

点评本题考查椭圆的标准方程，考查椭圆定义的应用，属于基础题．

练习册系列答案

4．函数f（x）=x²-2（a-1）x+2在区间[-1，4]上为单调函数，则a的取值范围是（-∞，0]∪[5，+∞）．

1．f（x）是奇函数，当x≥0时，f（x）=2x（1-x），则$f（-\frac{1}{2}）$=（　　）

8．已知4个数成等差数列，它们的和为20，中间两项之积为24，求这个4个数．

18．已知等差数列{a_n}的前n项和为S_n，若S₅=8，S₁₀=20，则S₁₅等于（　　）

	A．	命题“若x²=1，则x=1”的否命题为：“若x²=1，则x≠1”
	B．	若“p或q”为假命题，则“p且q”为真命题
	C．	命题“存在x₀∈R，使得x${\;}_{0}^{2}$+x₀+1＜0”的否定是：“对任意x∈R，均有x²+x+1＜0”
	D．	命题“在△ABC中，若A＞B，则sinA＞sinB”的逆否命题为真命题

2．离心率为$\frac{3}{4}$的椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0），P∈C，且P到椭圆的两个焦点距离之和为8则椭圆C的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{7}=1$．

4．设△ABC的内角A，B，C所对边的长分别为a，b，c，则下列命题正确的个数是．（　　）
①若ab＞c²，则$C＜\frac{π}{3}$
②若a+b＞2c，则$C＜\frac{π}{3}$
③若a³+b³=c³，则$C＜\frac{π}{2}$
④若（a+b）c＜2ab，则$C＞\frac{π}{2}$
⑤若（a²+b²）c²＜2a²b²，则$C＞\frac{π}{3}$．

试题分类