题目内容
4.函数f(x)=x2-2(a-1)x+2在区间[-1,4]上为单调函数,则a的取值范围是(-∞,0]∪[5,+∞).分析 求出函数的对称轴,利用已知条件列出不等式求解即可.
解答 解:函数f(x)=x2-2(a-1)x+2的对称轴为:x=a-1,
函数f(x)=x2-2(a-1)x+2在区间[-1,4]上为单调函数,
可得:a-1≤-1或a-1≥4,
解得a∈(-∞,0]∪[5,+∞).
故答案为:(-∞,0]∪[5,+∞).
点评 本题考查二次函数的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
9.已知圆 C1:x2+y2+2x+3y+1=0,圆 C2:x2+y2+4x+3y+2=0,圆C1与圆C2的位置关系为( )
| A. | 外切 | B. | 相离 | C. | 相交 | D. | 内切 |
16.若奇函数f(x)在[1,3]上是增函数,且最小值是1,则它在[-3,-1]上是( )
| A. | 增函数,最小值-1 | B. | 增函数,最大值-1 | C. | 减函数,最小值-1 | D. | 减函数,最大值-1 |
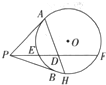 如图,已知点P是圆O外一点,过P做圆O的切线PA,PB,切点分别为A,B,过P做一条割线交圆O于E,F,若2PA=PF,取PF的中点D,连接AD,并延长交圆于H.
如图,已知点P是圆O外一点,过P做圆O的切线PA,PB,切点分别为A,B,过P做一条割线交圆O于E,F,若2PA=PF,取PF的中点D,连接AD,并延长交圆于H.