题目内容
3．过圆（x-1）2+y2=1外一点（3，0）作圆的切线，则切线的长为$\sqrt{3}$．分析 根据圆的标准方程，找出圆心坐标和半径，根据切线的性质得到三角形AMN为直角三角形，利用两点间的距离公式求出|AM|的长，再由半径|AN|，利用勾股定理即可求出切线长|MN|的长．
解答 解：（x-1）2+y2=1的圆心坐标A（1，0），半径|AN|=1，
又M（3，0）∴|AM|=2，
则切线长|MN|=$\sqrt{4-1}$=$\sqrt{3}$．
故答案为：$\sqrt{3}$．
点评 此题考查了直线与圆的位置关系，涉及的知识有两点间的距离公式，切线的性质，以及勾股定理，利用了数形结合的思想，当直线与圆相切时，圆心到直线的距离等于圆的半径，即直线与圆只有一个交点，熟练掌握切线性质是解本题的关键．
练习册系列答案
相关题目
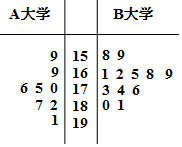某市旅游节需在A大学和B大学中分别招募8名和12名志愿者，这20名志愿者的身高（单位：cm）绘制出如图所示的茎叶图．若身高在175cm以上（包括175cm）定义为“高个子”，身高在175cm以下（不包括175cm）定义为“非高个子”，且只有B大学的“高个子”才能担任“兼职导游”．
如图，AC1是正方体ABCD-A1B1C1D1的对角线．