题目内容
解下列不等式:
(1)|
-3|>1
(2)|2x-1|+|3x-2|≥5.
(1)|
| 3x-2 |
(2)|2x-1|+|3x-2|≥5.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)利用绝对值不等式的运算性质可得
-3>1或
-3<-1,从而可得其解集;
(2)通过对x取值范围的讨论,去掉原不等式中的绝对值符号,解相应的不等式,最后取其并集即可.
| 3x-2 |
| 3x-2 |
(2)通过对x取值范围的讨论,去掉原不等式中的绝对值符号,解相应的不等式,最后取其并集即可.
解答:
解:(1)依题意得:
-3>1或
-3<-1,
∴
或
,
解得:
≤x<2或x>6,
∴原不等式的解集为{x|
≤x<2或x>6}.
(2)∵|2x-1|+|3x-2|≥5,
∴当x<
时,1-2x+2-3x≥5,故x≤-
;
当
≤x≤
时,2x-1+2-3x≥5,解得x≤-4,故x∈∅;
当x>
时,2x-1+3x-2≥5,解得x≥
.
∴原不等式的解集为:{x|x≤-
或x≥
}.
| 3x-2 |
| 3x-2 |
∴
|
|
解得:
| 2 |
| 3 |
∴原不等式的解集为{x|
| 2 |
| 3 |
(2)∵|2x-1|+|3x-2|≥5,
∴当x<
| 1 |
| 2 |
| 2 |
| 5 |
当
| 1 |
| 2 |
| 2 |
| 3 |
当x>
| 2 |
| 3 |
| 8 |
| 5 |
∴原不等式的解集为:{x|x≤-
| 2 |
| 5 |
| 8 |
| 5 |
点评:本题考查绝对值不等式的解法,着重考查等价转化思想与分类讨论思想的综合应用,考查运算能力,属于中档题.

练习册系列答案
相关题目
△ABC中,“A=B”是“tanA=tanB”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要条件 |
| D、既不充分又不必要 |
 某个公园有个池塘,其形状为直角三角形ABC,∠C=90°,AB=100米,BC=50米.
某个公园有个池塘,其形状为直角三角形ABC,∠C=90°,AB=100米,BC=50米.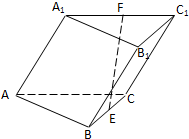 如图,斜三棱柱ABC-A1B1C1的侧棱长为
如图,斜三棱柱ABC-A1B1C1的侧棱长为