题目内容

5．⊙A，⊙B，⊙C两两外切，半径分别为2，3，10，则△ABC的形状是（　　）
A．锐角三角形B．钝角三角形C．直角三角形D．等腰三角形

分析 由勾股定理的逆定理可判定△ABC为直角三角形，可得答案．

解答 解：∵⊙A，⊙B，⊙C两两外切，它们的半径分别为2，3，10，
∴AB=2+3=5，BC=3+10=13，AC=2+10=12，
∵AB2+AC2=BC2，
∴△ABC为直角三角形．
故选：C．

点评 本题考查了相切两圆的性质、直角三角形的性质、勾股定理的逆定理，是基础知识要熟练掌握．

练习册系列答案
相关题目
15．已知集合A={-1，0，1}，B={x|0≤x≤1}，则A∩（∁RB）=（　　）
A．-1B．{-1}C．{1}D．{-1，1}
16．已知定义在R上的函数f（x）周期为T（常数），则命题“?x∈R，f（x）=f（x+T）”的否定是（　　）
A．?x∈R，f（x）≠f（x+T）B．?x∈R，f（x）≠f（x+T）C．?x∈R，f（x）=f（x+T）D．?x∈R，f（x）=f（x+T）
13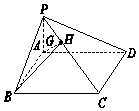．如图，H为四棱锥P-ABCD的棱PC的三等分点，且PH=$\frac{1}{2}$HC，点G在AH上，AG=mAH．四边形ABCD为平行四边形，若G，B，P，D四点共面，则实数m等于（　　）
A．$\frac{1}{4}$B．$\frac{4}{3}$P，DC．$\frac{3}{4}$D．$\frac{1}{2}$
20．已知函数f（x）是定义在[-e，0）∪（0，e]上的奇函数，当x∈[-e，0）时，f（x）=ax-ln（-x）．
（Ⅰ）求f（x）的解析式；
（Ⅱ）是否存在实数a，使得当x∈（0，e]时，f（x）的最大值是-3．如果存在，求出a的值，如果不存在，说明理由．
10．在△ABC中，若acosA=bsinB，则sinAcosA+cos2B=（　　）
A．1B．$\frac{1}{2}$C．-1D．$-\frac{1}{2}$
17．某企业节能降耗技术改造后，在生产某产品过程中记录的产量x（吨）与相应的生产能耗y（吨）的几组对应数据如表所示：
x3456
y2.534a
若根据表中数据得出y关于x的线性回归方程为y=0.7x+0.35，则表中a的值为4.5．
14．已知$\overrightarrow{a}$是单位向量，若$\overrightarrow{a}$•（$\overrightarrow{a}$+$\overrightarrow{b}$）=2，$\overrightarrow{b}$•（$\overrightarrow{a}$+$\overrightarrow{b}$）=4，则|$\overrightarrow{b}$|=$\sqrt{3}$．
15．若函数f（x）=$\left\{\begin{array}{l}{lo{g_{\frac{1}{2}}}x，0＜x≤1}\\{-{x^2}+4x-3，x＞1}\end{array}$，函数g（x）=f（x）-kx有两个零点，则k的值是（　　）
A．0或$4-2\sqrt{3}$B．$4+2\sqrt{3}$C．0D．$4±2\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网