题目内容
在平面直角坐标系xoy中,以O为极点,x轴的正半轴为极轴建立极坐标系,
(Ⅰ)已知曲线C1的极坐标方程为ρ=6cosθ,将曲线C1的极坐标方程化为直角坐标方程;
(Ⅱ)若在平面直角坐标系xoy中,曲线C2的参数方程为
(a>b>0,φ为参数).
已知曲线C2上的点M(1,
)及对应的参数ϕ=
.求曲线C2的直角坐标方程.
(Ⅰ)已知曲线C1的极坐标方程为ρ=6cosθ,将曲线C1的极坐标方程化为直角坐标方程;
(Ⅱ)若在平面直角坐标系xoy中,曲线C2的参数方程为
|
已知曲线C2上的点M(1,
| ||
| 2 |
| π |
| 3 |
考点:椭圆的参数方程,简单曲线的极坐标方程
专题:选作题,坐标系和参数方程
分析:(Ⅰ)曲线C的极坐标方程即 ρ2=6ρcosθ,根据 x=ρcosθ,y=ρsinθ,把它化为直角坐标方程.
(Ⅱ)将M(1,
)及对应的参数ϕ=
,代入曲线C2的参数方程,求出a、b的值,可得曲线C2的方程.
(Ⅱ)将M(1,
| ||
| 2 |
| π |
| 3 |
解答:
解:(I)曲线C的极坐标方程为ρ=6cosθ,即 ρ2=6ρcosθ,化为直角坐标方程为x2+y2=6x …(3分)
(Ⅱ)将M(1,
)及对应的参数ϕ=
,代入
,得
,
所以曲线C的方程为
+y2=1.…(7分)
(Ⅱ)将M(1,
| ||
| 2 |
| π |
| 3 |
|
|
所以曲线C的方程为
| x2 |
| 4 |
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,考查把参数方程化为普通方程的方法,属于基础题.

练习册系列答案
相关题目
命题“?x∈(0,+∞),x+
≥4”的否定为( )
| 4 |
| x |
A、?x∈(0,+∞),x+
| ||
B、?x∈(0,+∞),x+
| ||
C、?x∈(0,+∞),x+
| ||
D、?x∈(0,+∞),x+
|
若命题p:2是偶数,命题q:2是3的约数,则下列结论中正确的是( )
| A、“p∨q”为假 |
| B、“p∨q”为真 |
| C、“p∧q”为真 |
| D、以上都不对 |
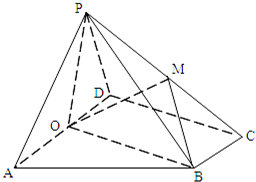 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD中点,M是棱PC上的点,AD=2BC.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD中点,M是棱PC上的点,AD=2BC. 如图,已知向量
如图,已知向量