题目内容
下列说法:
①命题“?x∈R,2x≤0”的否定是“?x∈R,2x>0”;
②关于x的不等式a<sin2x+
恒成立,则a的取值范围是a<3;
③对于函数f(x)=
(a∈R且a≠0),则有当a=1时,?k∈(1,+∞),使得函数g(x)=f(x)-kx在R上有三个零点;
④
dx≤
dx}
其中正确的是 .
①命题“?x∈R,2x≤0”的否定是“?x∈R,2x>0”;
②关于x的不等式a<sin2x+
| 2 |
| sin2x |
③对于函数f(x)=
| ax |
| 1+|x| |
④
| ∫ | 1 0 |
| 1-x2 |
| ∫ | e 1 |
| 1 |
| x |
其中正确的是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用命题的否定即可判断出;
②令sin2x=t∈[0,1],f(t)=t+
,利用导数研究函数的单调性;
③对于函数f(x)=
(a∈R且a≠0),则有当a=1时,若k∈(1,+∞),利用导数研究函数的单调性奇偶性即可判断出;
④利用微积分基本定理计算出即可判断出.
②令sin2x=t∈[0,1],f(t)=t+
| 2 |
| t |
③对于函数f(x)=
| ax |
| 1+|x| |
④利用微积分基本定理计算出即可判断出.
解答:
解:①命题“?x∈R,2x≤0”的否定是“?x∈R,2x>0”,正确;
②令sin2x=t∈[0,1],f(t)=t+
,f′(t)=1-
<0,因此函数f(t)在t∈[0,1]单调递减,∴f(t)≥f(1)=3,则a的取值范围是a<3,正确;
③对于函数f(x)=
(a∈R且a≠0),当a=1时,假设k∈(1,+∞),则当x>0时,g(x)=
-kx,g′(x)=
-k<0,于是函数g(x)单调递减,∴g(x)<g(0)=0,即当x>0时,函数g(x)无零点,由于函数g(x)为奇函数,因此x<0,也无零点,因此函数g(x)只有一个零点;
④
dx=
×π×12=
,
dx=lnx
=1,∴
dx≤
dx,正确.
其中正确的是 ①②④.
故答案为:①②④.
②令sin2x=t∈[0,1],f(t)=t+
| 2 |
| t |
| 2 |
| t2 |
③对于函数f(x)=
| ax |
| 1+|x| |
| x |
| 1+x |
| 1 |
| (1+x)2 |
④
| ∫ | 1 0 |
| 1-x2 |
| 1 |
| 4 |
| π |
| 4 |
| ∫ | e 1 |
| 1 |
| x |
| | | e 1 |
| ∫ | 1 0 |
| 1-x2 |
| ∫ | e 1 |
| 1 |
| x |
其中正确的是 ①②④.
故答案为:①②④.
点评:本题考查了利用导数研究函数的单调性、微积分基本定理、函数的奇偶性、简易逻辑的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
若命题p:2是偶数,命题q:2是3的约数,则下列结论中正确的是( )
| A、“p∨q”为假 |
| B、“p∨q”为真 |
| C、“p∧q”为真 |
| D、以上都不对 |
下列直线中与x-y+1=0平行的是( )
| A、x+y=-1 |
| B、x+y=1 |
| C、2x-2y=-2 |
| D、2x-2y=2 |
 如图,已知向量
如图,已知向量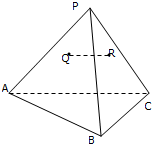 如图,已知P为△ABC所在平面内一点,Q、R是△PAB、△PBC的重心,求证:直线QR∥平面ABC.
如图,已知P为△ABC所在平面内一点,Q、R是△PAB、△PBC的重心,求证:直线QR∥平面ABC.