题目内容
6.在一个锐二面角的一个面内有一点,它到棱的距离等于到另一个平面的距离的2倍,则二面角大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 点P是锐二面角α-l-β中平面α内一点,PA⊥l,交l于点A,PB⊥β,交β于点B,从而得到AB⊥l,∠PAB是二面角α-l-β的平面角,由此能求出二面角的大小.
解答 解:如图,点P是锐二面角α-l-β中平面α内一点,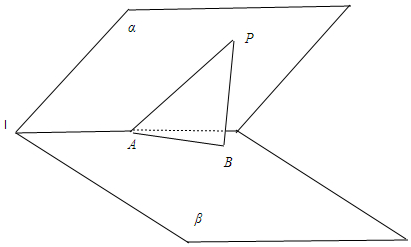
PA⊥l,交l于点A,PB⊥β,交β于点B,
∴AB⊥l,∴∠PAB是二面角α-l-β的平面角,
∵点P到棱的距离等于到另一个平面的距离的2倍,
∴PA=2PB,
∴sin∠PAB=$\frac{PB}{PA}$=$\frac{1}{2}$,
∴∠PAB=30°.
∴二面角的大小是30°.
故选:A.
点评 本题考查二面角的大小的求法,是中档题,解题时要认真审题,注意三垂线定理的合理运用.

练习册系列答案
相关题目
5.下列命题中,真命题是( )
| A. | ?x∈R,x2≥x | |
| B. | 命题“若x=1,则x2=1”的逆命题 | |
| C. | ?α0,β0∈R,使得sin(α0+β0)=sinα0+sinβ0 | |
| D. | 命题“若x≠y,则sinx≠siny”的逆否命题 |
6.若数列{an}满足$({2n+3}){a_{n+1}}-({2n+5}){a_n}=({2n+3})({2n+5})lg({1+\frac{1}{n}})$,且a1=5,则数列$\left\{{\frac{a_n}{2n+3}}\right\}$的第100项为( )
| A. | 2 | B. | 3 | C. | 1+lg99 | D. | 2+lg99 |
14.若△ABC是边长为1的等边三角形,且$\overrightarrow{AD}$=2$\overrightarrow{DB}$,2$\overrightarrow{AE}$=$\overrightarrow{EC}$,则$\overrightarrow{CD}$$•\overrightarrow{BE}$=( )
| A. | -$\frac{1}{9}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{7}{18}$ |
18.定义$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,则$|{\begin{array}{l}{sin{{50}°}}&{cos{{40}°}}\\{-\sqrt{3}tan{{10}°}}&1\end{array}}|$=( )
| A. | 2sin10° | B. | -1 | C. | $\sqrt{3}$ | D. | 0 |
16. 观察如图,则第( )行的各数之和等于20152.
观察如图,则第( )行的各数之和等于20152.
 观察如图,则第( )行的各数之和等于20152.
观察如图,则第( )行的各数之和等于20152.| A. | 2014 | B. | 2016 | C. | 1007 | D. | 1008 |