题目内容
17.直线a,b和平面α,β满足α∥β,a?α,b?β,则直线a,b的关系是( )| A. | 平行 | B. | 相交 | C. | 异面 | D. | 平行或异面 |
分析 以正方体为载体,列举直线a,b的关系,能求出结果.
解答  解:如图,在正方体ABCD-A1B1C1D1中,平面ABCD∥平面A1B1C1D1,
解:如图,在正方体ABCD-A1B1C1D1中,平面ABCD∥平面A1B1C1D1,
AB?平面ABCD,A1B1?平面A1B1C1D1,AB∥A1B1,
AB?ABCD,A1D1?平面A1B1C1D1,AB与A1D1异面,
∵直线a,b和平面α,β满足α∥β,a?α,b?β,
∴直线a,b的关系是平行或异面.
故选:D.
点评 本题考查两条直线的位置关系,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知z1=m+i,z2=1-2i,若$\frac{{z}_{1}}{{z}_{2}}$为实数,则实数m的值为( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
6.已知函数f(x)=x3+ax2+bx+c,x∈[-3,3]的图象过原点,且在点(1,f(1))和点(-1,f(-1))处的切线斜率为-2,则f(x)=( )
| A. | 是奇函数 | B. | 是偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 是非奇非偶函数 |
7.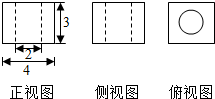 如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体的表面积是( )
如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体的表面积是( )
 如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体的表面积是( )
如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体的表面积是( )| A. | 80-2π | B. | 80 | C. | 80+4π | D. | 80+6π |
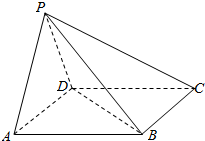 如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰三角形∠APD=90°,且平面PAD⊥平面ABCD
如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰三角形∠APD=90°,且平面PAD⊥平面ABCD