题目内容
7.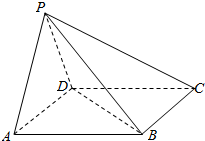 如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰三角形∠APD=90°,且平面PAD⊥平面ABCD
如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰三角形∠APD=90°,且平面PAD⊥平面ABCD(Ⅰ)求证:PA⊥PC;
(Ⅱ)若AD=2,AB=4,求三棱锥P-ABD的体积;
(Ⅲ)在条件(Ⅱ)下,求四棱锥P-ABCD外接球的表面积.
分析 (Ⅰ)由已知推导出CD⊥AD,CD⊥面PAD,从而PA⊥面PCD,进而PA⊥PC.
(Ⅱ)取AD中点E,连结PE,推导出PE是棱锥P-ABD的高,由此能求出三棱锥P-ABD的体积.
(Ⅲ)连结AC,交BD于O,由OA=OB=OC=OD=$\sqrt{5}$,得外接球的半径R=$\sqrt{5}$,由此能求出四棱锥P-ABCD的外接球的表面积.
解答 (本小题满分13分)
证明:(Ⅰ)∵面PAD⊥面ABCD,CD⊥AD,∴CD⊥AD,
∴CD⊥面PAD,
又CD?平面PCD,面PAD∩面PCD=PD,
∴PA⊥面PCD,
∴PA⊥PC.
解:(Ⅱ) 取AD中点E,连结PE,
取AD中点E,连结PE,
∵PA=PD,∴PE⊥AD,
又面PAD⊥面ABCD,∴PE⊥面ABCD,
∴PE是棱锥P-ABD的高,
在等腰直角三角形PAD中,AD=2,∴PE=1,
Rt△ABD中,AB=4,AD=2,∴${S}_{△ABD}=\frac{1}{2}×2×4=4$,
∴${V}_{P-ABD}=\frac{1}{3}{S}_{△ABD}•PE=\frac{1}{3}×4×1$=$\frac{4}{3}$.
(Ⅲ)连结AC,交BD于O,
∵ABCD是矩形,∴OA=OB=OC=OD=$\sqrt{5}$,
∴O为四棱锥P-ABCD的外接球的球心,且外接球的半径R=$\sqrt{5}$,
∴四棱锥P-ABCD的外接球的表面积S=4π($\sqrt{5}$)2=20π.
点评 本题考查异面直线垂直的证明,考查三棱锥的体积和四棱锥外接球的表面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
18.空间四点A、B、C、D满足|$\overline{AB}$|=3,|$\overrightarrow{BC}$|=7,|$\overrightarrow{CD}$|=11,|$\overrightarrow{DA}$|=9,则$\overrightarrow{AC}$•$\overrightarrow{BD}$的取值为( )
| A. | 只有一个 | B. | 有二个 | C. | 有四个 | D. | 有无穷多个 |
19.以下命题正确的是( )
| A. | 经过空间中的三点,有且只有一个平面 | |
| B. | 空间中,如果两个角的两条边分别对应平行,那么这两个角相等 | |
| C. | 空间中,两条异面直线所成角的范围是(0,$\frac{π}{2}$] | |
| D. | 如果直线l平行于平面α内的无数条直线,则直线l平等于平面α |
17.直线a,b和平面α,β满足α∥β,a?α,b?β,则直线a,b的关系是( )
| A. | 平行 | B. | 相交 | C. | 异面 | D. | 平行或异面 |

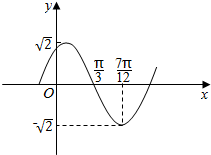 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数f(x)的解析式为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{3}$),或f(x)=$\sqrt{2}$sin(2x-$\frac{2π}{3}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数f(x)的解析式为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{3}$),或f(x)=$\sqrt{2}$sin(2x-$\frac{2π}{3}$).