题目内容
12.在锐角△ABC中,内角A、B、C的对边分别是a、b、c,且cos(B+C)=-$\frac{\sqrt{3}}{3}$sin2A.(1)求A;
(2)设a=7,b=5,求△ABC的面积.
分析 (1)由已知式子可得sinA,由锐角三角形可得;
(2)由正弦定理可得sinB,进而可得cosB,再由和差角的三角函数可得sinC,代入面积公式可得.
解答 解:(1)∵在锐角△ABC中cos(B+C)=-$\frac{\sqrt{3}}{3}$sin2A,
∴-cosA=-$\frac{\sqrt{3}}{3}$•2sinAcosA,
∴sinA=$\frac{\sqrt{3}}{2}$,A=$\frac{π}{3}$;
(2)由正弦定理可得sinB=$\frac{bsinA}{a}$=$\frac{5\sqrt{3}}{14}$,
∴cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{11}{14}$,
∴sinC=sin(A+B)=sinAcosB+cosAsinB
=$\frac{\sqrt{3}}{2}×\frac{11}{14}$+$\frac{1}{2}×\frac{5\sqrt{3}}{14}$=$\frac{4\sqrt{3}}{7}$,
∴△ABC的面积S=$\frac{1}{2}$absinC=$\frac{1}{2}$×7×5×$\frac{4\sqrt{3}}{7}$=10$\sqrt{3}$
点评 本题考查正弦定理,涉及三角形的面积公式以及和差角的三角函数公式,属中档题.

练习册系列答案
相关题目
3.设a=log30.3,b=20.3,c=0.32则( )
| A. | c>b>a | B. | c>a>b | C. | b>c>a | D. | b>a>c |
17.直线a,b和平面α,β满足α∥β,a?α,b?β,则直线a,b的关系是( )
| A. | 平行 | B. | 相交 | C. | 异面 | D. | 平行或异面 |
4.由直线y=2x及曲线y=4-2x2围成的封闭图形的面积为( )
| A. | 1 | B. | 3 | C. | 6 | D. | 9 |
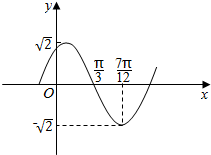 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数f(x)的解析式为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{3}$),或f(x)=$\sqrt{2}$sin(2x-$\frac{2π}{3}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数f(x)的解析式为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{3}$),或f(x)=$\sqrt{2}$sin(2x-$\frac{2π}{3}$).