题目内容
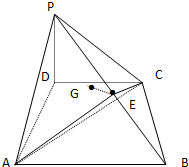 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠CDA=∠DAB=90°,PD⊥底面ABCD,PD=AD,CD=1,AB=2,E是PB中点,点E在平面ACP上的射影是△ACP
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠CDA=∠DAB=90°,PD⊥底面ABCD,PD=AD,CD=1,AB=2,E是PB中点,点E在平面ACP上的射影是△ACP的重心G.
(1)求PB与平面ACP所成角的正弦值;
(2)求二面角B-AC-E的平面角的正弦值.
考点:二面角的平面角及求法,直线与平面所成的角
专题:计算题,空间角
分析:(1)连结PG,则PG是PE在面ACP的射影,即∠EPG是PB与平面ACP所成的角,求出EG,PE,即可求PB与平面ACP所成角的正弦值;
(2)点E作底面ABCD的垂线,垂足为H,过点E作AC的垂线,垂足为I,连接HI,则∠HIE即为二面角B-AC-E的平面角,求出EH,EI,即可求二面角B-AC-E的平面角的正弦值.
(2)点E作底面ABCD的垂线,垂足为H,过点E作AC的垂线,垂足为I,连接HI,则∠HIE即为二面角B-AC-E的平面角,求出EH,EI,即可求二面角B-AC-E的平面角的正弦值.
解答:
 解:(1)连结PG,则PG是PE在面ACP的射影,
解:(1)连结PG,则PG是PE在面ACP的射影,
即∠EPG是PB与平面ACP所成的角.
设F为PA中点,连结EF、FD,
∵E,F分别是PA,PB的中点,底面ABCD是直角梯形,
∴EF∥CD,EF=CD,
∵CD⊥平面PAD,
∴DCEF为矩形,∴G∈CF.
∵EF=1,∴FC=
.
∴EC=
,EG=
=
,
∵PE=
,
∴sin∠EPG=
=
;
(2)过点E作底面ABCD的垂线,垂足为H,则EH∥PD,且EH=1.
过点E作AC的垂线,垂足为I,连接HI,则∠HIE即为二面角B-AC-E的平面角.
由于CE∥DF,而DF⊥面PAB,∴CE⊥AE,CE⊥PB,则CE=
,AE=
,
∴EI=
=
,
∴sin∠HIE=
=
=
∴二面角B-AC-E的平面角的正弦值是
.
 解:(1)连结PG,则PG是PE在面ACP的射影,
解:(1)连结PG,则PG是PE在面ACP的射影,即∠EPG是PB与平面ACP所成的角.
设F为PA中点,连结EF、FD,
∵E,F分别是PA,PB的中点,底面ABCD是直角梯形,
∴EF∥CD,EF=CD,
∵CD⊥平面PAD,
∴DCEF为矩形,∴G∈CF.
∵EF=1,∴FC=
| 3 |
∴EC=
| 2 |
1×
| ||
|
| ||
| 3 |
∵PE=
| 3 |
∴sin∠EPG=
| EG |
| PE |
| ||
| 3 |
(2)过点E作底面ABCD的垂线,垂足为H,则EH∥PD,且EH=1.
过点E作AC的垂线,垂足为I,连接HI,则∠HIE即为二面角B-AC-E的平面角.
由于CE∥DF,而DF⊥面PAB,∴CE⊥AE,CE⊥PB,则CE=
| 2 |
| 3 |
∴EI=
| ||||
|
| ||
| 5 |
∴sin∠HIE=
| EH |
| EI |
| 1 | ||||
|
| ||
| 6 |
∴二面角B-AC-E的平面角的正弦值是
| ||
| 6 |
点评:本题考查空间角的计算,考查学生的计算能力,正确作出空间角是关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
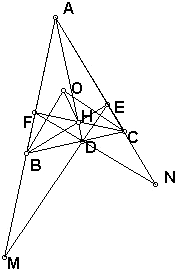 如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OB⊥DF.
如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OB⊥DF.