题目内容
已知A(1,2),B(3,4),C(5,0),求:
(1)求△ABC的边长;
(2)∠BAC的正弦值.
(1)求△ABC的边长;
(2)∠BAC的正弦值.
考点:两点间距离公式的应用,余弦定理
专题:计算题,直线与圆
分析:(1)利用两点间的距离公式求△ABC的边长;
(2)利用正弦函数求∠BAC的正弦值.
(2)利用正弦函数求∠BAC的正弦值.
解答:
解:(1)∵A(1,2),B(3,4),C(5,0),
∴|AB|=
=2
,|BC|=
=2
,|AC|=
=2
;
(2)由(1)知,|BC|=|AC|,△ABC为等腰三角形,底边上是高为
=3
,
∴sin∠BAC=
=
.
∴|AB|=
| (3-1)2+(4-2)2 |
| 2 |
| (5-3)2+(0-4)2 |
| 5 |
| (5-1)2+(0-2)2 |
| 5 |
(2)由(1)知,|BC|=|AC|,△ABC为等腰三角形,底边上是高为
| 20-2 |
| 2 |
∴sin∠BAC=
3
| ||
2
|
3
| ||
| 10 |
点评:本题考查两点间的距离公式,考查学生的计算能力,正确运用两点间的距离公式是关键.

练习册系列答案
相关题目
设P是?ABCD对角线的交点,O为空间任意一点(不在平面ABCD上),则
+
+
+
等于( )
| OA |
| OB |
| OC |
| OD |
A、4
| ||
B、6
| ||
C、2
| ||
D、
|
若函数f(x)=x3-bx,(b∈R)在区间(1,2)上有零点,则b的取值范围是( )
| A、(4,+∞) |
| B、(1,4) |
| C、(-4,-1) |
| D、(-∞,1) |
 。
。 ,求
,求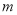 的取值范围。
的取值范围。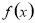 的最值,并给出最值时对应的
的最值,并给出最值时对应的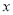 的值。
的值。