题目内容
设P是?ABCD对角线的交点，O为空间任意一点（不在平面ABCD上），则
+
+
+
等于（ ）
| OA |
| OB |
| OC |
| OD |
A、4
| ||
B、6
| ||
C、2
| ||
D、
|
考点：向量的加法及其几何意义
专题：平面向量及应用
分析：
=
+
，
=
+
，
=
+
，
=
+
，相加后相反向量抵消即得4
．
| OA |
| OP |
| PA |
| OB |
| OP |
| PB |
| OC |
| OP |
| PC |
| OD |
| OP |
| PD |
| OP |
解答：
解：如图，
=
+
，
=
+
，
=
+
，
=
+
，
因为P是平行四边形ABCD对角线的交点，
所以
与
、
与
互为相反向量，
所以
+
+
+
=
+
+
+
+
+
+
+
=4
+(
+
+
+
)
=4
，
故选：A．
解：如图，| OA |
| OP |
| PA |
| OB |
| OP |
| PB |
| OC |
| OP |
| PC |
| OD |
| OP |
| PD |
因为P是平行四边形ABCD对角线的交点，
所以
| PA |
| PC |
| PB |
| PD |
所以
| OA |
| OB |
| OC |
| OD |
=
| OP |
| PA |
| OP |
| PB |
| OP |
| PC |
| OP |
| PD |
=4
| OP |
| PA |
| PC |
| PB |
| PD |
=4
| OP |
故选：A．
点评：本题考查向量的加法运算，将向量转化为两个向量的和，然后抵消掉相反向量是解题的关键，属基础题．
练习册系列答案
相关题目
的定义域是（ ）
B. 
C. 
D. 
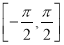上随机取一个
，
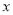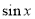的值介于
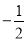与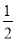
之间的概率为（ ）
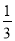（B）
（C）
（D）
如图，正方体ABCD-A1B1C1D1中，E、F分别是CD、CC1的中点．证明：EF∥平面AB1D1．
如图，在三棱锥P-ABC中，AB=5，BC=4，AC=3，点D是线段PB的中点，平面PAC⊥平面ABC．