题目内容
椭圆Γ:
+
=1(a>b>0)的左右焦点分别为F1、F2,已知椭圆Γ上的点P(
,
)到F1、F2的距离之和为2
;
(1)求椭圆Γ的方程;
(2)若椭圆上两点C、D关于点M(1,
)对称,求直线CD的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
(1)求椭圆Γ的方程;
(2)若椭圆上两点C、D关于点M(1,
| 1 |
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)由椭圆Γ上的点P(
,
)到两焦点F1、F2的距离之和为2
,可得
+
=1,2a=2
,a2=b2+c2,解出即可.
(2)设C(x1,y1),D(x2,y2),设P是直线CD上的任意一点,由
+
=1,
+
=1,相减可得:
+(y1+y2)(y1-y2)=1,利用中点坐标公式、斜率计算公式即可得出.
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
| 16 |
| 9a2 |
| 1 |
| 9b2 |
| 2 |
(2)设C(x1,y1),D(x2,y2),设P是直线CD上的任意一点,由
| ||
| 2 |
| y | 2 1 |
| ||
| 2 |
| y | 2 2 |
| (x1+x2)(x1-x2) |
| 2 |
解答:
解:(1)∵椭圆Γ上的点P(
,
)到两焦点F1、F2的距离之和为2
,
∴
+
=1,2a=2
,a2=b2+c2,
解得a=
,b=1,c=1.
∴椭圆Γ的方程为
+y2=1;
(2)设C(x1,y1),D(x2,y2),设P是直线CD上的任意一点,可得
=1,
=
,
=
(x≠1).
∵
+
=1,
+
=1,
相减可得:
+(y1+y2)(y1-y2)=1,
∴1+
=0,(x1≠x2).
∴1+
=0,
化为x+y-
=0,当x=1时也成立.
∴直线CD的方程为x+y-
=0.
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
∴
| 16 |
| 9a2 |
| 1 |
| 9b2 |
| 2 |
解得a=
| 2 |
∴椭圆Γ的方程为
| x2 |
| 2 |
(2)设C(x1,y1),D(x2,y2),设P是直线CD上的任意一点,可得
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| 1 |
| 2 |
| y1-y2 |
| x1-x2 |
y-
| ||
| x-1 |
∵
| ||
| 2 |
| y | 2 1 |
| ||
| 2 |
| y | 2 2 |
相减可得:
| (x1+x2)(x1-x2) |
| 2 |
∴1+
| y1-y2 |
| x1-x2 |
∴1+
y-
| ||
| x-1 |
化为x+y-
| 3 |
| 2 |
∴直线CD的方程为x+y-
| 3 |
| 2 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为“点差法”、中点坐标公式、斜率计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
如图,在四面体ABCD中,若截面PQMN是正方形,则在下列命题中,错误的为( )

| A、AC⊥BD |
| B、AC=BD |
| C、AC∥截面PQMN |
| D、异面直线PM与BD所成的角为45° |
已知实数a和b,记f(a,b)=
,g(a,b)=
,那么下列结论中不能恒成立的是( )
| a+b+|a-b| |
| 2 |
| a+b-|a-b| |
| 2 |
| A、f(a,b)=f(b,a) |
| B、g(a,b)=g(b,a) |
| C、g(a,f(b,c))=f(g(a,b),g(b,c)) |
| D、f(a,f(b,c))=f(f(a,b),c) |
 是( )
是( )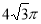 ,则该正方体的
,则该正方体的 如图,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1. 如图,正方体ABCD-A1B1C1D1中,E、F分别是CD、CC1的中点.证明:EF∥平面AB1D1.
如图,正方体ABCD-A1B1C1D1中,E、F分别是CD、CC1的中点.证明:EF∥平面AB1D1.