题目内容
(本小题满分12分)设函数 。
。
(1)求 ,求
,求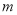 的取值范围。
的取值范围。
(2)求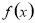 的最值,并给出最值时对应的
的最值,并给出最值时对应的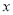 的值。
的值。
(1) ,(2)当
,(2)当 时
时 取得最小值
取得最小值 ,当
,当 时,
时, 取得最大值12.
取得最大值12.
【解析】
试题分析:(1)由于 在
在 上是增函数,根据
上是增函数,根据 的范围,求出
的范围,求出 的范围;(2)利用换元法把函数化为
的范围;(2)利用换元法把函数化为 ,画出抛物线可以看到,
,画出抛物线可以看到, 在
在 上是减函数,而在
上是减函数,而在 上是增函数,当
上是增函数,当 ,即
,即 时,
时, 取得最小值
取得最小值 ,当当
,当当 ,即
,即 时,
时, 取得最大值12.
取得最大值12.
试题解析:(1)因为 ,
, 为增函数,所以
为增函数,所以 ,即
,即 的取值范围是
的取值范围是 。
。
(2)由 得:
得:

 ,
,
又 ,所以当
,所以当 ,即
,即 时
时 取得最小值
取得最小值 ,
,
当 ,即
,即 时,
时, 取得最大值12。
取得最大值12。
考点:1.对数函数的图象与性质;2.换元法;3.二次函数的最值;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,若动点
,若动点 在函数
在函数 图象上,则
图象上,则 的最小值为 .
的最小值为 .
 是( )
是( ) 的定义域是( )
的定义域是( ) B.
B.  C.
C.  D.
D. 
 ,
, __________。
__________。 是
是 上的减函数,则
上的减函数,则 的取值范围是( )
的取值范围是( ) C.
C.  D.
D. 
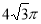 ,则该正方体的
,则该正方体的