题目内容
下列判断正确的是（ ）
A、若向量
| ||||
| B、单位向量都相等 | ||||
| C、共线的向量，若起点不同，则终点一定不同 | ||||
| D、模为0的向量的方向是不确定的 |
考点：命题的真假判断与应用
专题：平面向量及应用
分析：A中，向量
与
共线时，A，B，C，D四点不一定共线，判定A错误；
B中，由向量相等的定义判定单位向量不一定都相等，得出B错误；
C中，由共线向量的定义判定C错误；
D中，由零向量的方向是任意的判定D正确．
| AB |
| CD |
B中，由向量相等的定义判定单位向量不一定都相等，得出B错误；
C中，由共线向量的定义判定C错误；
D中，由零向量的方向是任意的判定D正确．
解答：
解：对于A，向量
与
是共线向量时，A，B，C，D四点不一定共线，
如平行四边形的对边是共线向量，但四点不共线；∴A错误．
对于B，单位向量的模长相等，方向不一定相同，
∴单位向量不一定都相等；∴B错误．
对于C，共线的向量，起点不同时，终点也可能相同；∴C错误．
对于D，模为0的向量是零向量，它的方向是不确定的；∴D正确．
综上，正确的命题是D．
故选：D．
| AB |
| CD |
如平行四边形的对边是共线向量，但四点不共线；∴A错误．
对于B，单位向量的模长相等，方向不一定相同，
∴单位向量不一定都相等；∴B错误．
对于C，共线的向量，起点不同时，终点也可能相同；∴C错误．
对于D，模为0的向量是零向量，它的方向是不确定的；∴D正确．
综上，正确的命题是D．
故选：D．
点评：本题考查了平面向量的应用问题，解题时应熟练地掌握向量共线的概念，向量相等与单位向量和零向量的概念等知识，是基础题．
练习册系列答案
相关题目
P为椭圆
+
=1上一点，F1、F2为该椭圆的两个焦点，若∠F1PF2=60°，则
•
=（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| PF1 |
| PF2 |
| A、3 | ||
B、
| ||
C、2
| ||
| D、2 |
若集合A={0，1，2，3}，B={0，2，4}，则集合A∪B=（ ）
| A、{1，2} |
| B、{1，2，3，4} |
| C、{0，1，2，3，4} |
| D、{0} |
正三棱锥的高是
，侧棱长为
，那么侧面与底面所成的二面角是（ ）
| 3 |
| 7 |
| A、60° | B、30° |
| C、45° | D、75° |
已知空间四边形ABCD每条边和对角线长都等于a，点E、F、G分别是AB、AD、DC的中点，则a2是下列哪个选项的计算结果（ ）
A、2
| ||||
B、2
| ||||
C、2
| ||||
D、2
|
某人朝正东方走xkm后，向左转150°，然后朝新方向走3km，结果它离出发点恰好
km，那么x等于（ ）
| 3 |
A、
| ||||
B、2
| ||||
C、
| ||||
| D、3 |
在棱长为3的正方体内任取一个点，则这个点到各面的距离大于1的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示是函数f（x）的导函数f′（x）的图象，则下列判断中正确的是（ ）
| A、函数f（x）在区间（-2，0）上是减函数 |
| B、函数f（x）在区间（1，3）上是减函数 |
| C、函数f（x）在区间（0，2）上是减函数 |
| D、函数f（x）在区间（3，4）上是增函数 |
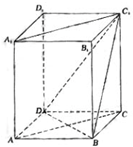如图，四棱柱ABCD-A1B1C1D1的底面是正方形，且侧棱和底面垂直．