题目内容
已知空间四边形ABCD每条边和对角线长都等于a，点E、F、G分别是AB、AD、DC的中点，则a2是下列哪个选项的计算结果（ ）
A、2
| ||||
B、2
| ||||
C、2
| ||||
D、2
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题意先判断相应向量的夹角，然后利用向量的数量积的定义化简各个式子即可判断
解答：
解：由题意可得，＜
，
＞=＜
，
＞=120°
∴2
•
=2|
||
|cos120°=-a2
2
•
=2|
||
|cos120°=2a2×cos120°=-a2．
∵FG∥AC且FG=
AC，EF∥BD且EF=
BD
∴2
•
=
2=a2，2
•
=
•CB=|
||
|cos120°=-
a2
故选：C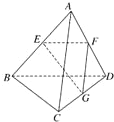
| BC |
| CA |
| AD |
| DB |
∴2
| BC |
| CA |
| BC |
| CA |
2
| AD |
| DB |
| AD |
| DB |
∵FG∥AC且FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴2
| FG |
| AC |
| AC |
| EF |
| CB |
| BD |
| BD |
| CB |
| 1 |
| 2 |
故选：C
点评：本题考查棱锥的结构特征，两个向量的数量积的定义，体现了数形结合的数学思想，解题的关键是准确判断各向量的夹角．
练习册系列答案
相关题目
设f（x）是定义在R上的奇函数，且f（2）=0，当x＞0时，有
＜0恒成立，则不等式f（x）＞0的解集是（ ）
| xf′(x)-f(x) |
| x2 |
| A、（-2，0）∪（2，+∞） |
| B、（-2，0）∪（0，2） |
| C、（-∞，-2）∪（2，+∞） |
| D、（-∞，-2）∪（0，2） |
已知空间向量ABCD中，
=
，
=
，
=
，则
等于（ ）
| AB |
| a |
| CB |
| b |
| AD |
| c |
| CD |
A、
| ||||||
B、-
| ||||||
C、-
| ||||||
D、-
|
有以下四种变换方式：
①向左平移
个单位长度，再将每个点的横坐标缩短为原来的
；
②向右平移
个单位长度，再将每个点的横坐标缩短为原来的
；
③每个点的横坐标缩短为原来的
，向右平移
个单位长度；
④每个点的横坐标缩短为原来的
，向左平移
个单位长度；
其中能将y=sinx的图象变换成函数y=sin（2x+
）的图象的是（ ）
①向左平移
| π |
| 4 |
| 1 |
| 2 |
②向右平移
| π |
| 8 |
| 1 |
| 2 |
③每个点的横坐标缩短为原来的
| 1 |
| 2 |
| π |
| 8 |
④每个点的横坐标缩短为原来的
| 1 |
| 2 |
| π |
| 8 |
其中能将y=sinx的图象变换成函数y=sin（2x+
| π |
| 4 |
| A、①和③ | B、①和④ |
| C、②和④ | D、②和③ |
设a＞0，b＞0，则以下不等式中不一定成立的是（ ）
| A、a2+b2+2≥2a+2b | ||||
| B、ln（ab+1）≥0 | ||||
C、
| ||||
| D、a3+b3≥2ab2 |
下列判断正确的是（ ）
A、若向量
| ||||
| B、单位向量都相等 | ||||
| C、共线的向量，若起点不同，则终点一定不同 | ||||
| D、模为0的向量的方向是不确定的 |
若集合M={y|y=2x}，P={x|y=
}，M∩P=（ ）
| x-1 |
| A、[1，+∞） |
| B、[0，+∞） |
| C、（0，+∞） |
| D、（1，+∞） |
cos
的值是（ ）
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|