题目内容
设10件产品中有4件次品,6件正品,求下列事件的概率.
(1)有放回的任取三件至少有2件次品;
(2)从中依次取5件恰有2件次品;
(3)从中任取2件都是次品;
(4)从中任取5件恰有2件次品.
(1)有放回的任取三件至少有2件次品;
(2)从中依次取5件恰有2件次品;
(3)从中任取2件都是次品;
(4)从中任取5件恰有2件次品.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)保证有两次取到次品即可,所以概率为
×
=
;
(2)先求出依次取5件恰有2件次品的取法,再求出取出5件的取法;
(3)取2次,每次取到的都是次品;
(4)先求出取5件恰有2件次品的取法,再求出取出5件的取法.
| 4 |
| 10 |
| 4 |
| 10 |
| 4 |
| 25 |
(2)先求出依次取5件恰有2件次品的取法,再求出取出5件的取法;
(3)取2次,每次取到的都是次品;
(4)先求出取5件恰有2件次品的取法,再求出取出5件的取法.
解答:
解:(1)有放回的抽取,每次去到次品的概率为
,
抽三次至少有两次品.就是保证有两次取到次品,三次中的另外一次不用管,
所以至少有两次品的概率为
×
=
;
(2)从中依次取5件恰有2件次品的取法有
•
•
•
•
=6×5×4×4×3种,
从中依次取出5件的取法有
=10×9×8×7×6种,
所以从中依次取5件恰有2件次品的概率为
=
;
(3)取2次,每次抽到的都是次品,
故所求概率为
×
=
;
(4)十件产品中取5件的取法有
=252种,
其中恰好2件次品的取法有
×
=120种,
所以从中任取5件恰有2件次品的概率为
=
.
| 4 |
| 10 |
抽三次至少有两次品.就是保证有两次取到次品,三次中的另外一次不用管,
所以至少有两次品的概率为
| 4 |
| 10 |
| 4 |
| 10 |
| 4 |
| 25 |
(2)从中依次取5件恰有2件次品的取法有
| C | 1 4 |
| C | 1 3 |
| C | 1 6 |
| C | 1 5 |
| C | 1 4 |
从中依次取出5件的取法有
| A | 5 10 |
所以从中依次取5件恰有2件次品的概率为
| 6×5×4×4×3 |
| 10×9×8×7×6 |
| 1 |
| 21 |
(3)取2次,每次抽到的都是次品,
故所求概率为
| 4 |
| 10 |
| 3 |
| 9 |
| 2 |
| 15 |
(4)十件产品中取5件的取法有
| C | 5 10 |
其中恰好2件次品的取法有
| C | 2 4 |
| C | 3 6 |
所以从中任取5件恰有2件次品的概率为
| 120 |
| 252 |
| 10 |
| 21 |
点评:本题考查求概率问题,注意区分(2)与(4).

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
关于幂函数f(x)=x3,若0<x1<x2,则f(
)、
的大小关系( )
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
A、f(
| ||||
B、f(
| ||||
C、f(
| ||||
| D、无法确定 |
已知f(cosx)=cos17x,则f(sinx)的结果是( )
| A、sin17x | ||
| B、cos17x | ||
C、sin
| ||
D、cos
|
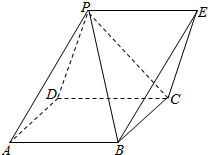 有一个所有棱长均为a的正四棱锥P-ABCD,还有一个所有棱长均为a的正三棱锥,将此三棱锥的一个面与正四棱锥的一个侧面完全重合的黏在一起,得到一个如图所示的多面体;
有一个所有棱长均为a的正四棱锥P-ABCD,还有一个所有棱长均为a的正三棱锥,将此三棱锥的一个面与正四棱锥的一个侧面完全重合的黏在一起,得到一个如图所示的多面体; 为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作标本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩.
为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作标本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩.