题目内容
7.若x,y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x-y≤0}\\{x+y-4≤0}\end{array}\right.$,则z=2x-y+1的取值范围为( )| A. | [0,1] | B. | [0,2] | C. | [0,3] | D. | [2,3] |
分析 由约束条件作出可行域,数形结合得到最优解,求出最优解的坐标,代入目标函数得答案.
解答 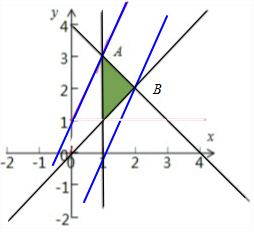 解:x,y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x-y≤0}\\{x+y-4≤0}\end{array}\right.$
解:x,y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x-y≤0}\\{x+y-4≤0}\end{array}\right.$
对应的区域如图:
当直线z=2x-y+1经过A时,目标函数最小,
当经过B时最大;由$\left\{\begin{array}{l}{x-1=0}\\{x+y=4}\end{array}\right.$得到A(1,3),
由$\left\{\begin{array}{l}{x+y-4=0}\\{x-y=0}\end{array}\right.$,解得B(2,2)
所以目标函数z=2x-y+1的最大值为2×2-2+1=3,
最小值为2×1-3+1=0;
故目标函数z=2x-y+1的取值范围为[0,3];
故选:C.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.在等差数列{an}中,a3+a9=18-a6,Sn表示数列{an}的前n项和,则S11=( )
| A. | 66 | B. | 99 | C. | 198 | D. | 297 |
18.若0<m<n<2,e为自然对数的底数,则下列各式中一定成立的是( )
| A. | men<nem | B. | men>nem | C. | mlnn>nlnm | D. | mlnn<nlnm |
15.在长为8cm的线段AB上任取一点C,作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积小于15cm2的概率为( )
| A. | $\frac{8}{15}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
2.已知函数f(x)=2sinωx+1(ω>0)在区间[-$\frac{π}{2}$,$\frac{2π}{3}$]上是增函数,则ω的取值范围是( )
| A. | (0,$\frac{3}{4}$] | B. | (0,1] | C. | [$\frac{3}{4}$,1] | D. | [$\frac{3}{2}$,1] |
12.已知$|{\overrightarrow a}|=1$,$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$,$({\overrightarrow a+2\overrightarrow b})•\overrightarrow a=3$,则$|{\overrightarrow b}|$的值是( )
| A. | 3 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
16.已知双曲线过点(2,3),其中一条渐近线方程为$y=\sqrt{3}x$,则双曲线的标准方程是( )
| A. | $\frac{{7{x^2}}}{16}-\frac{y^2}{12}=1$ | B. | $\frac{y^2}{3}-\frac{x^2}{2}=1$ | C. | ${x^2}-\frac{y^2}{3}=1$ | D. | $\frac{{3{y^2}}}{23}-\frac{x^2}{23}=1$ |