题目内容
2.函数f(x)=x+$\frac{1}{x}$+a有零点,则实数a的取值范围是a≥2或a≤-2.分析 由题意知x+$\frac{1}{x}$+a=0有解,从而求利用基本不等式求解.
解答 解:∵函数f(x)=x+$\frac{1}{x}$+a有零点,
∴x+$\frac{1}{x}$+a=0有解,
∵x+$\frac{1}{x}$≥2或x+$\frac{1}{x}$≤-2;
∴a≥2或a≤-2;
故答案为;a≥2或a≤-2.
点评 本题考查了函数的零点与方程的根的关系应用及基本不等式的应用.

练习册系列答案
相关题目
12.已知数{an}满a1=0,an+1=an+2n,那a2016的值是( )
| A. | 2014×2015 | B. | 2015×2016 | C. | 2014×2016 | D. | 2015×2015 |
14.过抛物线y2=2px(p>0)的焦点F的直线交抛物线于A,B两点,点O是原点,如果|BF|=3,|BF|>|AF|,$∠BFO=\frac{2π}{3}$,那么|AF|的值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 3 | D. | 6 |
 如图,底面ABCD为矩形,侧棱PA⊥底面ABCD,$AB=\sqrt{3}$,BC=1,PA=2,求直线AC与PB所成角的余弦值.
如图,底面ABCD为矩形,侧棱PA⊥底面ABCD,$AB=\sqrt{3}$,BC=1,PA=2,求直线AC与PB所成角的余弦值.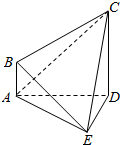 如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=3AB.
如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=3AB.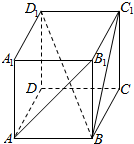 如图,在正方体ABCD-A1B1C1D1中.求:
如图,在正方体ABCD-A1B1C1D1中.求: