题目内容
若f(x)=x2+(a-1)x+1是定义在R上的偶函数,则实数a= .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数奇偶性的定义建立方程f(-x)=f(x)即可求解a的值.
解答:
解:∵f(x)=x2+(a-1)x+1是定义在R上的偶函数,
∴f(-x)=f(x),
即f(-x)=x2-(a-1)x+1=x2+(a-1)x+1,
∴-(a-1)=a-1,
∴a-1=0,
解得a=1.
故答案为:1.
∴f(-x)=f(x),
即f(-x)=x2-(a-1)x+1=x2+(a-1)x+1,
∴-(a-1)=a-1,
∴a-1=0,
解得a=1.
故答案为:1.
点评:本题主要考查函数奇偶性的应用,利用函数奇偶性的定义建立方程是解决本题的关键.

练习册系列答案
相关题目
已知f(x)=
是定义在R上x1≠x2,恒有
>0的函数,求a的取值范围是( )
|
| f(x1)-f(x2) |
| x1-x2 |
| A、[2,3) |
| B、(1,3) |
| C、(1,+∞) |
| D、(1,2] |
 若一个底面是正三角形的三棱柱的三视图如图所示,则其体积等于
若一个底面是正三角形的三棱柱的三视图如图所示,则其体积等于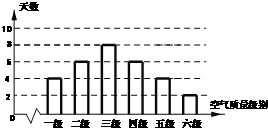 根据空气质量指数AQI(为整数)的不同,可将空气质量分级如下表:
根据空气质量指数AQI(为整数)的不同,可将空气质量分级如下表: