题目内容
若A、B为互斥事件，给出下列结论
①P（A）+P（B）＜1；
②P（A）+P（B）=1；
③P（A）+P（B）≤1；
④P（A•B）=0，
则正确结论个数为（ ）
①P（A）+P（B）＜1；
②P（A）+P（B）=1；
③P（A）+P（B）≤1；
④P（A•B）=0，
则正确结论个数为（ ）
| A、4 | B、3 | C、2 | D、1 |
考点：互斥事件与对立事件
专题：探究型
分析：由已知中，A，B为互斥事件，则A∪B为随机事件，当A，B为对立事件时，A∪B为必然事件，根据随机事件及对立事件的概率我们易得到结论．
解答：
解：由已知中A，B为互斥事件，
由互斥事件概率加法公式可得：P（A）+P（B）≤1，
当A，B为对立事件时，P（A）+P（B）=1，
当A，B互斥不对立时，P（A）+P（B）＜1，
∵A，B为互斥事件，
∴A•B为不可能事件，则P（A•B）=0．
∴命题①错误；
命题②错误；
命题③正确；
命题④正确．
故选：C．
由互斥事件概率加法公式可得：P（A）+P（B）≤1，
当A，B为对立事件时，P（A）+P（B）=1，
当A，B互斥不对立时，P（A）+P（B）＜1，
∵A，B为互斥事件，
∴A•B为不可能事件，则P（A•B）=0．
∴命题①错误；
命题②错误；
命题③正确；
命题④正确．
故选：C．
点评：本题考查的知识点是互斥事件概率加法公式，其中当A，B为对立事件时，A∪B为必然事件，概率为1，易被忽略，此题是基础题．
练习册系列答案
阅读快车系列答案
相关题目
在面积为9的正方形ABCD内部随机取一点P，则能使△PAB的面积大于3的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
（坐标系与参数方程选做题）如图所示的极坐标系中，以M（4，
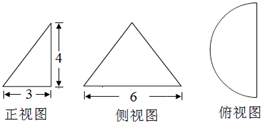某几何体的三视图如图所示（单位：cm），则其体积和表面积分别是（ ）| A、6πcm3和12（1+π）cm2 |
| B、6πcm3和12πcm2 |
| C、12πcm3和12（1+π）cm2 |
| D、12πcm3和12πcm2 |
若直线y=x+m与圆x2+y2+4x+2=0有两个不同的公共点，则实数m的取值范围是（ ）
| A、（0，4） | ||||
| B、（-4，0） | ||||
C、(-2-
| ||||
D、(2-
|