题目内容
为了得到函数y=sin2x的图象,只需把函数y=sin(2x-
)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:把函数y=sin(2x-
)变形为y=sin2(x-
),可知要得函数y=sin(2x-
)的图象,只需把函数y=sin2x的图象向右平移
个单位,取逆过程得答案.
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
解答:
解:∵y=sin(2x-
)=sin2(x-
),
∴要得函数y=sin(2x-
)的图象,只需把函数y=sin2x的图象向右平移
个单位,
反之,要得函数y=sin2x的图象,只需把函数y=sin(2x-
)的图象向左平移
个单位.
故选:C.
| π |
| 3 |
| π |
| 6 |
∴要得函数y=sin(2x-
| π |
| 3 |
| π |
| 6 |
反之,要得函数y=sin2x的图象,只需把函数y=sin(2x-
| π |
| 3 |
| π |
| 6 |
故选:C.
点评:本题考查y=Asin(ωx+φ)型函数的图象平移问题,三角函数的平移原则为左加右减上加下减,是基础题.

练习册系列答案
相关题目
已知a,b∈[-1,1],则函数f(x)=ax+b在区间(1,2)上存在一个零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=sinx-cosx的图象可由函数y=sinx+cosx的图象经过下列哪种变换得到( )
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
在约束条件
下,目标函数z=x+2y的最大值为( )
|
| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
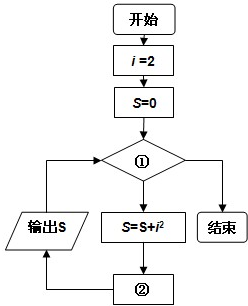 如图分别表示输出22,22+42,22+42+62,…,22+42+62+…+20142值得过程的一个程序框图,那么在图中①②分别填上( )
如图分别表示输出22,22+42,22+42+62,…,22+42+62+…+20142值得过程的一个程序框图,那么在图中①②分别填上( )| A、i≤2014,i=i+1 |
| B、i≤1007,i=i+1 |
| C、i≤2014,i=i+2 |
| D、i≤1007,i=i+2 |
设变量x,y满足不等式组
,则2x+3y的最大值等于( )
|
| A、1 | B、10 | C、41 | D、50 |
 如图是某青年歌手大奖赛上七位评委为某选手打出的分数的茎叶图(其中m为数字0-9中的一个).若这组数据的中位数和平均数相等,则m=
如图是某青年歌手大奖赛上七位评委为某选手打出的分数的茎叶图(其中m为数字0-9中的一个).若这组数据的中位数和平均数相等,则m=