题目内容
已知正四棱锥的底边和侧棱长均为4
,则该正四棱锥的外接球的表面积为= .
| 2 |
考点:球的体积和表面积
专题:空间位置关系与距离
分析:正四棱锥外接球的球心在它的底面的中心,然后根据勾股定理解出球的半径,最后根据球的表面积公式求解即可.
解答:
解:如图,设正四棱锥底面的中心为O,则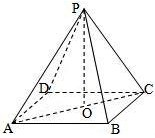
在直角三角形ABC中,AC=
×AB=8,
∴AO=CO=4,
在直角三角形PAO中,PO=
=4,
∴正四棱锥的各个顶点到它的底面的中心的距离都为4,
∴正四棱锥外接球的球心在它的底面的中心,且球半径r=4,
球的表面积S=4πr2=64π,
故答案为:64π.

在直角三角形ABC中,AC=
| 2 |
∴AO=CO=4,
在直角三角形PAO中,PO=
| PA2-AO2 |
∴正四棱锥的各个顶点到它的底面的中心的距离都为4,
∴正四棱锥外接球的球心在它的底面的中心,且球半径r=4,
球的表面积S=4πr2=64π,
故答案为:64π.
点评:本题主要考查球的表面积,球的内接体问题,考查计算能力和空间想象能力,利用条件求出球的半径是解决本题的关键.

练习册系列答案
相关题目
若实数x,y满足x2+y2-1=0,则z=
的取值范围是( )
| y-1 |
| x+2 |
A、[-
| ||
B、[0,
| ||
C、[-2,-
| ||
D、[-
|
为了得到函数y=sin2x的图象,只需把函数y=sin(2x-
)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|