题目内容
已知数列{an}的前n项和Sn=-an-(
)n-1+2 (n为正整数).
(1)令bn=2nan,求证数列{bn}是等差数列;
(2)求数列{an}的通项公式,并求数列{an}的前n项和Tn.
| 1 |
| 2 |
(1)令bn=2nan,求证数列{bn}是等差数列;
(2)求数列{an}的通项公式,并求数列{an}的前n项和Tn.
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(1)利用递推关系可得n≥2时,an=Sn-Sn-1=-an+an-1+(
)n-1,整理可得2nan=2n-1an-1+1,依题意即可证得数列{bn}是等差数列;
(2)由(1)知bn=n=2nan,可求得an=
,利用错位相减法即可求得数列{an}的前n项和Tn.
| 1 |
| 2 |
(2)由(1)知bn=n=2nan,可求得an=
| n |
| 2n |
解答:
(1)证明:在Sn=-an-(
)n-1+2中,令n=1,可得S1=-a1-1+2=a1,即a1=
…1分
当n≥2时,an=Sn-Sn-1=-an+an-1+(
)n-1,…3分
∴2an=an-1+(
)n-1,…4分
即2nan=2n-1an-1+1…5分
∵bn=2nan,
∴bn-bn-1=1(n≥2),.
又b1=2a1=1,
∴数列{bn}是首项和公差均为1的等差数列…7分
(2)解:由(1)知bn=1+(n-1)•1=n=2nan,
∴an=
…9分
Tn=
+
+
+…+
,
Tn=
+
+…+
+
…11分
∴
Tn=
+
+…+
-
=
-
=1-
-
…13分
∴Tn=2-
…14分
| 1 |
| 2 |
| 1 |
| 2 |
当n≥2时,an=Sn-Sn-1=-an+an-1+(
| 1 |
| 2 |
∴2an=an-1+(
| 1 |
| 2 |
即2nan=2n-1an-1+1…5分
∵bn=2nan,
∴bn-bn-1=1(n≥2),.
又b1=2a1=1,
∴数列{bn}是首项和公差均为1的等差数列…7分
(2)解:由(1)知bn=1+(n-1)•1=n=2nan,
∴an=
| n |
| 2n |
Tn=
| 1 |
| 21 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| n-1 |
| 2n |
| n |
| 2n+1 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| n |
| 2n+1 |
=
| ||||
1-
|
| n |
| 2n+1 |
| 1 |
| 2n |
| n |
| 2n+1 |
∴Tn=2-
| n+2 |
| 2n |
点评:本题考查数列的求和,着重考查递推关系的应用,考查等差关系的确定与错位相减法求和的应用,属于中档题.

练习册系列答案
相关题目
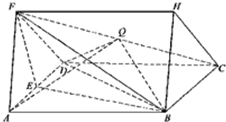 如图,三棱柱ADF-BCH中,侧面ABCD是菱形,FA=FD,∠BAD=60°,E是AD的中点,点Q在线段FC上.
如图,三棱柱ADF-BCH中,侧面ABCD是菱形,FA=FD,∠BAD=60°,E是AD的中点,点Q在线段FC上. 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDES,SA=AB=AE=2,BC=DE=
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDES,SA=AB=AE=2,BC=DE=