题目内容
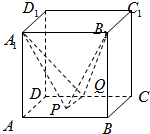 如图,设正方体ABCD-A1B1C1D1的棱长为1,P是底面ABCD上的动点,Q是线段DC上的动点,且四面体A1B1PQ的体积为
如图,设正方体ABCD-A1B1C1D1的棱长为1,P是底面ABCD上的动点,Q是线段DC上的动点,且四面体A1B1PQ的体积为| 1 |
| 8 |
A、 |
B、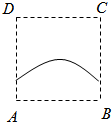 |
C、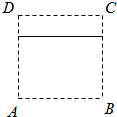 |
D、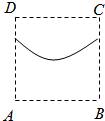 |
考点:轨迹方程
专题:探究型
分析:首先求出三角形A1B1Q的面积,把四面体A1B1PQ的体积转化为三棱锥P-A1B1Q的体积,由等积法求出P点到平面A1B1Q的距离,则可得到P点的轨迹.
解答:
解:如图,

当Q点在线段DC上运动时,Q到A1B1的距离即为两平行线DC与A1B1的距离,
∵正方体的棱长为1,∴DC与A1B1的距离为
.
设Q到A1B1的距离为h,则h=
,
∴S△A1B1Q=
A1B1•h=
.
再设P到平面A1B1Q的距离为h′,
∴VA1-B1PQ=VP-A1B1Q=
S△A1B1Q•h′=
×
h′=
,
∴h′=
>
.
∴P的轨迹为平面ABCD内与平面A1B1Q平行,且距离为
的一条线段.
故选:A.

当Q点在线段DC上运动时,Q到A1B1的距离即为两平行线DC与A1B1的距离,
∵正方体的棱长为1,∴DC与A1B1的距离为
| 2 |
设Q到A1B1的距离为h,则h=
| 2 |
∴S△A1B1Q=
| 1 |
| 2 |
| ||
| 2 |
再设P到平面A1B1Q的距离为h′,
∴VA1-B1PQ=VP-A1B1Q=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 8 |
∴h′=
3
| ||
| 8 |
| 1 |
| 2 |
∴P的轨迹为平面ABCD内与平面A1B1Q平行,且距离为
3
| ||
| 8 |
故选:A.
点评:本题考查了轨迹方程,考查了棱锥的体积公式,训练了“等积法”,是中档题.

练习册系列答案
相关题目
 如图是容量为100的样本的频率分布直方图,则样本数据在[14,18)内的频率和频数分别是( )
如图是容量为100的样本的频率分布直方图,则样本数据在[14,18)内的频率和频数分别是( )| A、0.24,24 |
| B、0.08,8 |
| C、0.32,32 |
| D、0.36,36 |
设x0是函数f(x)=lnx+x-4的零点,则x0所在的区间为( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
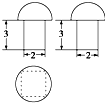 已知一个几何体的三视图如图所示,则该几何体的表面积为( )
已知一个几何体的三视图如图所示,则该几何体的表面积为( )| A、24+6π |
| B、24+4π |
| C、28+6π |
| D、28+4π |
若0<m<1,则( )
| A、logm(1+m)>logm(1-m) | ||||
| B、logm(1+m)>0 | ||||
| C、1-m>(1+m)2 | ||||
D、(1-m)
|
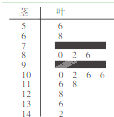 某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下: