题目内容
若0<m<1,则( )
| A、logm(1+m)>logm(1-m) | ||||
| B、logm(1+m)>0 | ||||
| C、1-m>(1+m)2 | ||||
D、(1-m)
|
考点:不等关系与不等式
专题:函数的性质及应用
分析:由0<m<1,可得对数函数y=logmx是(0,+∞)上的减函数,从而判定A、B是否正确;
可得1-m与(1+m)2的大小,判定C是否正确;
可得指数函数y=(1-m)x是定义域R上的减函数,从而判定D是否正确;
可得1-m与(1+m)2的大小,判定C是否正确;
可得指数函数y=(1-m)x是定义域R上的减函数,从而判定D是否正确;
解答:
解:①∵0<m<1,∴函数y=logmx是(0,+∞)上的减函数,又∵1+m>1-m>0,∴logm(1+m)<logm(1-m);∴A不正确;
②∵0<m<1,∴1+m>1,∴logm(1+m)<0;∴B不正确;
③∵0<m<1,∴0<1-m<1,1+m>1,∴1-m>(1+m)2;∴C不正确;
④∵0<m<1,∴0<1-m<1,∴函数y=(1-m)x是定义域R上的减函数,又∵
<
,∴(1-m)
>(1-m)
;∴D正确;
故选:D.
②∵0<m<1,∴1+m>1,∴logm(1+m)<0;∴B不正确;
③∵0<m<1,∴0<1-m<1,1+m>1,∴1-m>(1+m)2;∴C不正确;
④∵0<m<1,∴0<1-m<1,∴函数y=(1-m)x是定义域R上的减函数,又∵
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
故选:D.
点评:本题考查了应用指数函数与对数函数的单调性判定函数值的大小,是基础题.

练习册系列答案
相关题目
曲线y=xcosx在x=
处的切线的斜率是( )
| π |
| 3 |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
已知函数ft(x)=(x-t)2-t(t∈R),设a<b,f(x)=
,若函数f(x)+x+a-b有四个零点,则b-a的取值范围是( )
|
A、(2+
| ||
B、(0,2+
| ||
C、(0,2+
| ||
D、(2+
|
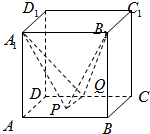 如图,设正方体ABCD-A1B1C1D1的棱长为1,P是底面ABCD上的动点,Q是线段DC上的动点,且四面体A1B1PQ的体积为
如图,设正方体ABCD-A1B1C1D1的棱长为1,P是底面ABCD上的动点,Q是线段DC上的动点,且四面体A1B1PQ的体积为