题目内容
已知数列a>0,b>0,a1=1,前P项和Sn=
an
(1)求{an}的通项公式;
(2)求数列{
}的前n项和.
| n+1 |
| 2 |
(1)求{an}的通项公式;
(2)求数列{
| an |
| 2n |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知得
=
,由此利用累乘法得
=n,从而an=n.
(2)设数列数列{
}的前n项和Tn,利用错位相减法能求出数列{
}的前n项和.
| an |
| an-1 |
| n |
| n-1 |
| an |
| a1 |
(2)设数列数列{
| an |
| 2n |
| an |
| 2n |
解答:
解:(1)∵Sn=
an∴Sn-1=
an-1(n≥2),
∴an=
an-
an-1,
即:
=
,
∴
=
,
=
…
=
,
累乘得:
=n,
∵a1=1,
∴an=n.
(2)设数列数列{
}的前n项和Tn,
则Tn=1•(
)1+2•(
)2+3•(
)3+…+(n-1)(
)n-1+n•(
)n,
Tn=1•(
)2+2•(
)3+3•(
)4+…+(n-1)(
)n+n•(
)n+1,
两式相减得:
Tn=(
)1+(
)2+(
)3+…+(
)n-n•(
)n+1=
-n•(
)n+1=1-(1+
)(
)n,
∴Tn=2-(n+2)(
)n.
| n+1 |
| 2 |
| n |
| 2 |
∴an=
| n+1 |
| 2 |
| n |
| 2 |
即:
| an |
| an-1 |
| n |
| n-1 |
∴
| a2 |
| a1 |
| 2 |
| 1 |
| a3 |
| a2 |
| 3 |
| 2 |
| an |
| an-1 |
| n |
| n-1 |
累乘得:
| an |
| a1 |
∵a1=1,
∴an=n.
(2)设数列数列{
| an |
| 2n |
则Tn=1•(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
两式相减得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
∴Tn=2-(n+2)(
| 1 |
| 2 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若△ABC的内角A、B、C的对边分别为a、b、c,且(a-b)2=c2-4,C=120°,则ab的值为( )
| A、4 | ||
B、
| ||
C、
| ||
D、8-4
|
已知集合M={x|x+1≥0},N={x|x2<4},则M∩N=( )
| A、(-∞,-1) |
| B、(2,+∞) |
| C、(-1,2) |
| D、[-1,2) |
已知函数①f(x)=5x2;②f(x)=5cosx;③f(x)=5ex;④f(x)=5lnx,其中对于f(x)定义域内的任意一个自变量x1,都存在唯一的自变量x2,使
=5成立的函数有( )个.
| f(x1)f(x2) |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知Sn为数列{an}的前n项和,且满足a1=1,anan+1=3n(n∈N+),则S2014=( )
| A、2×31007-2 | ||
| B、2×31007 | ||
C、
| ||
D、
|
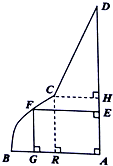 如图是一块镀锌铁皮的边角料ABCD,其中AB、CD、DA都是线段,曲线段BC是抛物线的一部分,且点B是该抛物线的顶点,BA所在直线是该抛物线的对称轴,经测量,AB=2米,AD=3米,AB⊥AD,点C到AD、AB的距离CH、CR的长均为1米,现要用这块边角料截一个矩形AEFG(其中点F在曲线段BC或线段CD上,点E在线段AD上,点G在线段AB上).设BG的长为x米,矩形AEFG的面积为S平方米.
如图是一块镀锌铁皮的边角料ABCD,其中AB、CD、DA都是线段,曲线段BC是抛物线的一部分,且点B是该抛物线的顶点,BA所在直线是该抛物线的对称轴,经测量,AB=2米,AD=3米,AB⊥AD,点C到AD、AB的距离CH、CR的长均为1米,现要用这块边角料截一个矩形AEFG(其中点F在曲线段BC或线段CD上,点E在线段AD上,点G在线段AB上).设BG的长为x米,矩形AEFG的面积为S平方米. 如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是AC上的一点,若AF⊥BE,垂足为F,求证:∠BFD=∠C.
如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是AC上的一点,若AF⊥BE,垂足为F,求证:∠BFD=∠C.