题目内容
17.已知△ABC的顶点A、B的坐标分别为(-$\sqrt{3}$,0)、($\sqrt{3}$,0),C为动点,且满足sinB+sinA=$\sqrt{2}$sinC.(1)求点C的轨迹L的方程;
(2)设M(x0,y0)是曲线L上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交曲线L于点P、Q.
①若直线OP、OQ的斜率均存在,并记为k1,k2,求证:k1k2为定值;
②试问OP2+OQ2是否为定值?若是,求出该值;若不是,请说明理由.
分析 (1)运用正弦定理和椭圆的定义可得,C的轨迹为以A,B为焦点的椭圆,且有a=$\sqrt{6}$,c=$\sqrt{3}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,即可得到所求轨迹方程;
(2))①由直线OP:y=k1x,OQ:y=k2x与圆M相切,运用圆心到直线的距离为半径,即可得到k1,k2为方程(x02-2)k2-2x0y0k+y02-2=0的两个不等的实根,运用韦达定理和点M在椭圆上,满足椭圆方程,化简即可得到所求定值;
②OP2+OQ2为定值9.讨论当直线OP,OQ的斜率均存在时,P(x1,y1),Q(x2,y2),运用①的结论,结合P,Q在椭圆上,满足椭圆方程,化简整理,由两点的距离公式即可得到定值9;当直线OP,OQ的斜率不存在时,圆M与x,y轴均相切,即可得到定值.
解答 解:(1)由sinB+sinA=$\sqrt{2}$sinC,可得|CA|+|CB|=$\sqrt{2}$|AB|,
即有|CA|+|CB|=2$\sqrt{6}$>2$\sqrt{3}$,
即有C的轨迹为以A,B为焦点的椭圆,
且a=$\sqrt{6}$,c=$\sqrt{3}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
可得轨迹L的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1(y≠0);
(2)①证明:由直线OP:y=k1x与圆M相切,可得$\frac{|{k}_{1}{x}_{0}-{y}_{0}|}{\sqrt{1+{{k}_{1}}^{2}}}$=$\sqrt{2}$,
即有(x02-2)k12-2x0y0k1+y02-2=0,
同理由直线OQ:y=k2x与圆M相切,
可得(x02-2)k22-2x0y0k2+y02-2=0,
即k1,k2为方程(x02-2)k2-2x0y0k+y02-2=0的两个不等的实根,
可得k1k2=$\frac{{{y}_{0}}^{2}-2}{{{x}_{0}}^{2}-2}$,
由M在椭圆上,可得$\frac{{x}_{{0}^{2}}}{6}$+$\frac{{{y}_{0}}^{2}}{3}$=1,即为y02=3-$\frac{1}{2}$x02,
即有k1k2=$\frac{1-\frac{1}{2}{{x}_{0}}^{2}}{{{x}_{0}}^{2}-2}$=-$\frac{1}{2}$;
②OP2+OQ2为定值9.
理由如下:当直线OP,OQ的斜率均存在时,P(x1,y1),Q(x2,y2),
由k1k2=-$\frac{1}{2}$,即y12y22=$\frac{1}{4}$x12x22,
由P(x1,y1),Q(x2,y2)在椭圆上,可得
$\frac{{{x}_{1}}^{2}}{6}$+$\frac{{{y}_{1}}^{2}}{3}$=1,$\frac{{{x}_{2}}^{2}}{6}$+$\frac{{{y}_{2}}^{2}}{3}$=1,
即y12=3-$\frac{1}{2}$x12,y22=3-$\frac{1}{2}$x22,
则(3-$\frac{1}{2}$x12)(3-$\frac{1}{2}$x22)=$\frac{1}{4}$x12x22,
即有x12+x22=6,
y12+y22=(3-$\frac{1}{2}$x12)+(3-$\frac{1}{2}$x22)=6-3=3,
即OP2+OQ2=9;
当直线OP,OQ的斜率不存在时,圆M与x,y轴均相切,
显然有OP2+OQ2=9.
综上可得,OP2+OQ2为定值9.
点评 本题考查轨迹方程的求法,注意运用椭圆定义,以及正弦定理,考查直线和圆心切的条件:d=r,以及点满足椭圆方程,考查两点的距离公式的运用,化简整理的运算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | {-1,0,1} | B. | {-1,1} | C. | {-1,1,2} | D. | {1,0} |
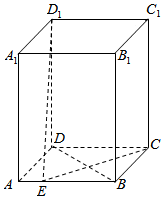 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱AA1⊥底面ABCD,已知AB=1,${A}{{A}_1}=\sqrt{3}$,E为AB上一个动点,则D1E+CE的最小值为( )
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱AA1⊥底面ABCD,已知AB=1,${A}{{A}_1}=\sqrt{3}$,E为AB上一个动点,则D1E+CE的最小值为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{10}$ | C. | $\sqrt{5}+1$ | D. | $2+\sqrt{2}$ |
 某市气象部门对该市中心城区近4年春节期间(每年均统计春节假期的前7天)的空气污染指数进行了统计分析,且按是否燃放鞭炮分成两组,得到如图的茎叶图,根据国家最新标准,空气污染指数不超过100的表示没有雾霾,超过100的表示有雾霾.
某市气象部门对该市中心城区近4年春节期间(每年均统计春节假期的前7天)的空气污染指数进行了统计分析,且按是否燃放鞭炮分成两组,得到如图的茎叶图,根据国家最新标准,空气污染指数不超过100的表示没有雾霾,超过100的表示有雾霾.(Ⅰ)若从茎叶图有雾霾的14天中随机抽取2天,用随机变量ξ表示被抽中且未燃放鞭炮的天数,求ξ的分布列及数学期望;
(Ⅱ)通过茎叶图填写下面的2×2列联表,并判断有多大的把握可以认为燃放鞭炮与产生雾霾有关?
| 燃放 | 未燃放 | 合计 | |
| 有雾霾 | |||
| 无雾霾 | |||
| 合计 |
独立性检验临界值表:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| x | 16 | 17 | 18 | 19 |
| y | 50 | 34 | 41 | 31 |
| A. | 26个 | B. | 27个 | C. | 28个 | D. | 29个 |