题目内容
12.在△ABC中,角A,B,C的对边分别为a,b,c,已知2ccosB=2a-b.(Ⅰ)求角C的大小;
(Ⅱ)若$c=\sqrt{3}$,b-a=1,求△ABC的面积.
分析 (Ⅰ)由题意和余弦定理可得a2+b2-c2=ab,再由余弦定理可得cosC,可得角C;
(Ⅱ)由已知数据和余弦定理可解得ab的值,代入三角形的面积公式可得.
解答 解:(Ⅰ)在△ABC中,由2ccosB=2a-b和余弦定理可得$2c\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=2a-b$,
∴a2+b2-c2=ab,∴$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=\frac{1}{2}$,
又C∈(0,π),∴$C=\frac{π}{3}$;
(Ⅱ)∵$C=\frac{π}{3}$,$c=\sqrt{3}$,∴由余弦定理可得a2+b2-ab=3,
又∵b-a=1,∴a2+a-2=0,∴a=1或a=-2(舍去),
∴a=1,b=2,$c=\sqrt{3}$,
∴△ABC的面积S=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{2}$
点评 本题考查正余弦定理解三角形,涉及三角形的面积公式,属基础题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
3.设椭圆的标准方程为$\frac{x^2}{9-k}+\frac{y^2}{5-k}=1$,若焦点在x轴上,则实数k的取值范围是( )
| A. | k>5 | B. | 5<k<9 | C. | k<5 | D. | k>9 |
7.在△ABC中,角A,B,C的对边分别为a,b,c.若sin(A-B)+sinC=$\sqrt{2}$sinA.
(Ⅰ)求角B的值;
(Ⅱ)若b=2,求a2+c2的最大值,并求取得最大值时角A,C的值.
(Ⅰ)求角B的值;
(Ⅱ)若b=2,求a2+c2的最大值,并求取得最大值时角A,C的值.
17.已知函数f(x)为奇函数,当x≥0时,f(x)=log2(x+l)+m,则f(1-$\sqrt{2}$)的值为( )
| A. | -$\frac{1}{2}$ | B. | -log2(2-$\sqrt{2}$) | C. | $\frac{1}{2}$ | D. | log2(2-$\sqrt{2}$) |
4.已知全集U={y|y=x3,x=-1,0,1,2},集合A={-1,1},B={1,8},则A∩(∁UB)=( )
| A. | {-1,1} | B. | {-1} | C. | {1} | D. | ∅ |
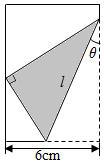 如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,那么折痕长度l取决于角θ的大小,探求l,θ之间的关系式,并导出用θ表示l的函数表达式.
如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,那么折痕长度l取决于角θ的大小,探求l,θ之间的关系式,并导出用θ表示l的函数表达式.