题目内容
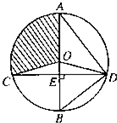
选修4-1几何证明选讲如图，已知⊙O的直径AB垂直于弦CD于E，连结AD、BD、OC、OD，且OD=5．
（Ⅰ）若sin∠BAD=
| 3 |
| 5 |
（Ⅱ）若∠ADO：∠EDO=4：1，求扇形OAC（阴影部分）的面积（结果保留π）．
考点：弦切角,与圆有关的比例线段
专题：立体几何
分析：（I）由⊙O的直径AB垂直于弦CD于E，利用垂径定理可得CE=ED．在Rt△ABD中，利用直角三角形的边角关系可得BD=ABsin∠BAD．再利用勾股定理可得AD=
．由等面积变形可得
AB×ED=
AD•BD，即可得出．
（II）设∠ODE=x，则∠ADO=4x，利用三角形外角定理可得∠EOD=∠OAD+∠ODE=8x．在Rt△EOD中，由于∠EOD+∠ODE=
，可得x=
．进而得到∠AOC=2∠ADC=
．再利用扇形的面积计算公式即可得出．
| AB2-AD2 |
| 1 |
| 2 |
| 1 |
| 2 |
（II）设∠ODE=x，则∠ADO=4x，利用三角形外角定理可得∠EOD=∠OAD+∠ODE=8x．在Rt△EOD中，由于∠EOD+∠ODE=
| π |
| 2 |
| π |
| 18 |
| 5π |
| 9 |
解答：
解：（I）∵⊙O的直径AB垂直于弦CD于E，∴CE=ED，∠ADB=90°．
在Rt△ABD中，∵sin∠BAD=
，∴BD=AB•sin∠BAD=10×
=6．
由勾股定理可得AD=
=
=8．
∵
AB×ED=
AD•BD，∴ED=
=
=4.8．
∴CD=2ED=9.6．
（II）设∠ODE=x，则∠ADO=4x，∵OA=OD，∴∠OAD=4x．
∴∠EOD=∠OAD+∠ODE=8x．
在Rt△EOD中，∠EOD+∠ODE=
，∴8x+x=
，解得x=
．
∴∠ADC=
，
∴∠AOC=2∠ADC=
．
∴扇形OAC（阴影部分）的面积S=
×
×52=
π．
在Rt△ABD中，∵sin∠BAD=
| 3 |
| 5 |
| 3 |
| 5 |
由勾股定理可得AD=
| AB2-AD2 |
| 102-62 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
| AD•BD |
| AB |
| 6×8 |
| 10 |
∴CD=2ED=9.6．
（II）设∠ODE=x，则∠ADO=4x，∵OA=OD，∴∠OAD=4x．
∴∠EOD=∠OAD+∠ODE=8x．
在Rt△EOD中，∠EOD+∠ODE=
| π |
| 2 |
| π |
| 2 |
| π |
| 18 |
∴∠ADC=
| 5π |
| 18 |
∴∠AOC=2∠ADC=
| 5π |
| 9 |
∴扇形OAC（阴影部分）的面积S=
| 1 |
| 2 |
| 5π |
| 9 |
| 125 |
| 18 |
点评：本题综合考查了圆的性质、垂径定理、直角三角形的边角关系、勾股定理、等面积变形、三角形外角定理、扇形的面积计算公式等基础知识与基本技能方法，属于基础题．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
己知某几何体的三视图如图所示，则该几何体的体积是（ ）
A、
| ||||
B、
| ||||
C、2
| ||||
D、2
|
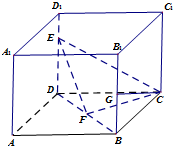如图，在棱长为1的正方体ABCD-A1B1C1D1中，点E是棱DD1上的动点，F，G分别是BD，BB1的中点．
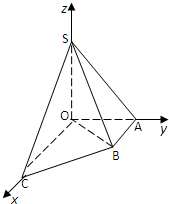如图直角梯形OABC中，∠COA=∠OAB=90°，OC=2，OA=AB=1，SO⊥平面OABC，SO=1，分别以OC，OA，OS为x轴、y轴、z轴建立直角坐标系O-xyz．
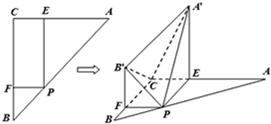如图，在△ABC中，∠C=90°，AC=BC=a，点P在边AB上，设
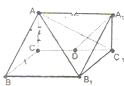已知三棱柱ABC-A1B1C1的底面为直角三角形，则棱与底面垂直，如图所示，D是棱CC1的中点，且∠ACB=90°，BC=1，AC=
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，∠ABC=90°，AD∥BC，且PA=AD=2，AB=BC=1，E为PD的中点．