题目内容
设f(x)=
(1+x)(ax2+bx+c),g(x)=-e -x+
-|ln(x+1)|+k
(1)若f(x)的图象关于x=-1对称,且f(1)=2,求f(x)的解析式;
(2)对于(1)中的f(x),讨论f(x)与g(x)的图象的交点个数.
| 1 |
| 2 |
| 1 |
| 2 |
(1)若f(x)的图象关于x=-1对称,且f(1)=2,求f(x)的解析式;
(2)对于(1)中的f(x),讨论f(x)与g(x)的图象的交点个数.
考点:函数的零点,函数解析式的求解及常用方法,二次函数的性质
专题:函数的性质及应用
分析:(1)由于f(x)的图象关于x=-1对称,可得f(x)为二次函数,a=0,且 b=c,故有f(x)=
(1+x)(bx+b).再根据f(1)=2,求得b=1,可得f(x)的解析式.
(2)f(x)与g(x)的图象的交点个数,即
(x+1)2=-e-x+
-|ln(x+1)|+k 的解的个数,
即直线y=k和函数
(x+1)2 +e-x+
+|ln(x+1)|的图象的交点个数.令h(x)=
(x+1)2 +e-x+
+|ln(x+1)|,利用导数求得函数的h(x)的单调区间,可得函数h(x)的值域,可得直线y=k和h(x)的图象的交点个数.
| 1 |
| 2 |
(2)f(x)与g(x)的图象的交点个数,即
| 1 |
| 2 |
| 1 |
| 2 |
即直线y=k和函数
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)由于f(x)=
(1+x)(ax2+bx+c)的图象关于x=-1对称,
故f(x)为二次函数,且对称轴为x=-1,故有a=0,且 b=c,故有f(x)=
(1+x)(bx+b).
再根据f(1)=2,求得b=1,故f(x)=
(x+1)2.
(2)f(x)与g(x)的图象的交点个数,即
(x+1)2=-e-x+
-|ln(x+1)|+k 的解的个数,
即k=
(x+1)2 +e-x+
+|ln(x+1)|的解得个数.
即直线y=k和函数
(x+1)2 +e-x+
+|ln(x+1)|的图象的交点个数.
令h(x)=
(x+1)2 +e-x+
+|ln(x+1)|,
当x>0时,ln(x+1)>0,
∵h′(x)=(1+x)-e-x+
+
≥2+e-x+
>0,
∴h′(x)>0,h(x)在(0,+∞)上是增函数.
当-1<x≤0时,ln(x+1)≤0,h′(x)=(1+x)-e-x+
-
,
∵(x+1)-
<0,e-x+
>0,∴h′(x)<0,
故h(x)在(-1,0]上是减函数.
∵h(0)=
+e
,当x趋于-1时,函数h(x)的值趋于正无穷大,
当x趋于正无穷大时,函数h(x)的值趋于正无穷大,
①故当k<
+e
时,直线y=k和函数h(x)的图象无交点,函数f(x)与g(x)的图象无交点;
②当k=
+e
时,直线y=k和函数h(x)的图象有唯一交点,函数f(x)与g(x)的图象有一个交点;
③当k>
+e
时,直线y=k和函数h(x)的图象有2个交点,函数f(x)与g(x)的图象有2个交点.
| 1 |
| 2 |
故f(x)为二次函数,且对称轴为x=-1,故有a=0,且 b=c,故有f(x)=
| 1 |
| 2 |
再根据f(1)=2,求得b=1,故f(x)=
| 1 |
| 2 |
(2)f(x)与g(x)的图象的交点个数,即
| 1 |
| 2 |
| 1 |
| 2 |
即k=
| 1 |
| 2 |
| 1 |
| 2 |
即直线y=k和函数
| 1 |
| 2 |
| 1 |
| 2 |
令h(x)=
| 1 |
| 2 |
| 1 |
| 2 |
当x>0时,ln(x+1)>0,
∵h′(x)=(1+x)-e-x+
| 1 |
| 2 |
| 1 |
| x+1 |
| 1 |
| 2 |
∴h′(x)>0,h(x)在(0,+∞)上是增函数.
当-1<x≤0时,ln(x+1)≤0,h′(x)=(1+x)-e-x+
| 1 |
| 2 |
| 1 |
| x+1 |
∵(x+1)-
| 1 |
| x+1 |
| 1 |
| 2 |
故h(x)在(-1,0]上是减函数.
∵h(0)=
| 1 |
| 2 |
| 1 |
| 2 |
当x趋于正无穷大时,函数h(x)的值趋于正无穷大,
①故当k<
| 1 |
| 2 |
| 1 |
| 2 |
②当k=
| 1 |
| 2 |
| 1 |
| 2 |
③当k>
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查用待定系数法求函数的解析式,二次函数的性质应用,体现了分类讨论、转化的数学思想,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知F是双曲线
-
=1(a>0)的右焦点,O为坐标原点,设P是双曲线C上一点,则∠POF的大小不可能是( )
| x2 |
| 3a2 |
| y2 |
| a2 |
| A、15° | B、25° |
| C、60° | D、165° |
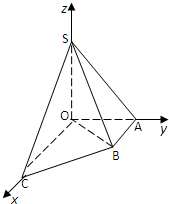 如图直角梯形OABC中,∠COA=∠OAB=90°,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,分别以OC,OA,OS为x轴、y轴、z轴建立直角坐标系O-xyz.
如图直角梯形OABC中,∠COA=∠OAB=90°,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,分别以OC,OA,OS为x轴、y轴、z轴建立直角坐标系O-xyz.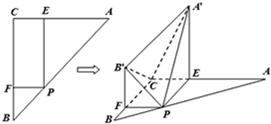 如图,在△ABC中,∠C=90°,AC=BC=a,点P在边AB上,设
如图,在△ABC中,∠C=90°,AC=BC=a,点P在边AB上,设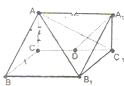 已知三棱柱ABC-A1B1C1的底面为直角三角形,则棱与底面垂直,如图所示,D是棱CC1的中点,且∠ACB=90°,BC=1,AC=
已知三棱柱ABC-A1B1C1的底面为直角三角形,则棱与底面垂直,如图所示,D是棱CC1的中点,且∠ACB=90°,BC=1,AC=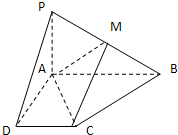 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=