题目内容
20.已知数列{an}中a1=2,a2=1,an+2=$\left\{\begin{array}{l}{\frac{2{a}_{n+1}}{{a}_{n}},{a}_{n+1}≥2}\\{\frac{4}{{a}_{n}},{a}_{n+1}<2}\end{array}\right.$(n∈N*),Sn是数列{an}的前n项和,则S778=2020.分析 通过计算出前几项的值确定周期,进而计算可得结论.
解答 解:依题意,a1=2,a2=1,a3=$\frac{4}{{a}_{1}}$=$\frac{4}{2}$=2,
a4=$\frac{2{a}_{3}}{{a}_{2}}$=$\frac{2×2}{1}$=4,a5=$\frac{2{a}_{4}}{{a}_{3}}$=$\frac{2×4}{2}$=4,
a6=$\frac{2{a}_{5}}{{a}_{4}}$=$\frac{2×4}{4}$=2,a7=$\frac{2{a}_{6}}{{a}_{5}}$=$\frac{2×2}{4}$=1,
…
∴数列{an}是以5为周期的周期数列,
∵778=5×155+3,
∴S778=(2+1+2+4+4)×155+(2+1+2)=2020,
故答案为:2020.
点评 本题考查数列的通项及前n项和,找出周期是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
8.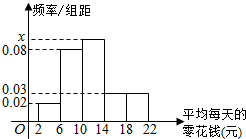 为了了解学生平均每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观,某校从高一年级1000名学生中随机抽取100名进行了调查,将所得数据整理后,画出频率分布直方图(如图),据此估计高一年级每天零花钱在[6,14)内的学生数为( )
为了了解学生平均每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观,某校从高一年级1000名学生中随机抽取100名进行了调查,将所得数据整理后,画出频率分布直方图(如图),据此估计高一年级每天零花钱在[6,14)内的学生数为( )
 为了了解学生平均每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观,某校从高一年级1000名学生中随机抽取100名进行了调查,将所得数据整理后,画出频率分布直方图(如图),据此估计高一年级每天零花钱在[6,14)内的学生数为( )
为了了解学生平均每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观,某校从高一年级1000名学生中随机抽取100名进行了调查,将所得数据整理后,画出频率分布直方图(如图),据此估计高一年级每天零花钱在[6,14)内的学生数为( )| A. | 780 | B. | 680 | C. | 648 | D. | 460 |
15.己知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,右顶点和上顶点分别为A、B,过点F作x轴的垂线与椭圆在第一象限于点P,直线OP交AB于点Q,若|OQ|=|AQ|,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
12.若$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(x,2)且$\overrightarrow{a}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$),则x等于( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
9.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,则下列关系正确的是( )
| A. | |$\overrightarrow{a}•\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$| | B. | |$\overrightarrow{a}•\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| | ||
| C. | |$\overrightarrow{a}•\overrightarrow{b}$|≥|$\overrightarrow{a}$||$\overrightarrow{b}$| | D. | 以上答案都不正确 |
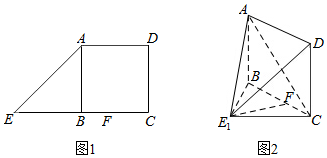 如图1,在直角梯形ADCE中,AD∥EC,EC=2BC,∠ADC=90°,AB⊥EC,点F为线段BC上的一点.将△ABE沿AB折到△ABE1的位置,使E1F⊥BC,如图2.
如图1,在直角梯形ADCE中,AD∥EC,EC=2BC,∠ADC=90°,AB⊥EC,点F为线段BC上的一点.将△ABE沿AB折到△ABE1的位置,使E1F⊥BC,如图2.