为了了解学生平均每天零花钱的数量.以便引导学生树立正确的消费观.某校从高一年级1000名学生中随机抽取100名进行了调查.将所得数据整理后.画出频率分布直方图.据此估计高一年级每天零花钱在[6.14)内的学生数为( )A．780B．680C．648D．460 题目和参考答案——青夏教育精英家教网—

题目内容

8．

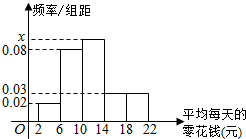为了了解学生平均每天零花钱的数量（钱数取整数元），以便引导学生树立正确的消费观，某校从高一年级1000名学生中随机抽取100名进行了调查，将所得数据整理后，画出频率分布直方图（如图），据此估计高一年级每天零花钱在[6，14）内的学生数为（　　）

A．

780

B．

680

C．

648

D．

460

分析根据频率分布直方图，利用频率和为1，求出在[6，14）内的频率与频数即可．

解答解：根据频率分布直方图得，每天零花钱在[6，14）内的频率为
1-（0.02+0.03+0.03）×4=0.68；
对应的学生数是1000×0.68=680；
故选：B．

点评本题考查了频率分布直方图的应用问题，是基础题目．

练习册系列答案

$[\frac{{3\sqrt{10}}}{10}，\;2]$

19．求证：（$\frac{1}{si{n}^{4}α}$-1）（$\frac{1}{co{s}^{4}α}$-1）≥9．

16．方程e^x-x-2=0的一个根所在的区间（k，k+1）（k∈N），则k的值为（　　）

3．求下列函数周期：
（1）y=|sinx|+sinx
（2）y=2sin（2x+$\frac{π}{3}$），x∈[-$\frac{π}{6}$，$\frac{π}{6}$]
（3）y=$\frac{cosx-2}{cosx-1}$
（4）y=2cos（2x+$\frac{π}{3}$），x∈R．

13．

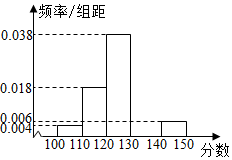2015-2016学年高二A班50名学生在其中数学测试中（满分150分），成绩都介于100分到150分之间，将测试结果按如下方式分成五组，第一组[100，110），第二组[110，120），…，第五组[140，150），按上述分组方法得到的频率分布直方图如图所示，
（1）将频率分布直方图补充完整；
（2）若成绩大于等于110分且小于130分规定为良好，求该班在这次数学测试中成绩为良好的人数；
（3）请根据频率分布直方图，估计样本数据的众数和中位数（精确到0.1）．

20．已知数列{a_n}中a₁=2，a₂=1，a_n+2=$\left\{\begin{array}{l}{\frac{2{a}_{n+1}}{{a}_{n}}，{a}_{n+1}≥2}\\{\frac{4}{{a}_{n}}，{a}_{n+1}＜2}\end{array}\right.$（n∈N^*），S_n是数列{a_n}的前n项和，则S₇₇₈=2020．

17．下列直线中，平行于直线x-y+1=0且与圆x²+y²=4相切的是（　　）

18．已知sin（θ+$\frac{π}{2}$）＜0，cos（θ-$\frac{π}{2}$）＞0，则下列不等式关系必定成立的是（　　）

sin$\frac{θ}{2}$＞cos$\frac{θ}{2}$

D．

sin$\frac{θ}{2}$＜cos$\frac{θ}{2}$

试题分类