题目内容
9.写出等差数列3,7,11,…的第4项和第10项.分析 由已知先求出首项a1=3,公差d=7-3=4,由此能求出第4项和第10项.
解答 解:等差数列3,7,11,…中,
首项a1=3,公差d=7-3=4,
∴a4=a1+3d=3+3×4=15,
a10=a1+9d=3+9×4=39.
点评 本题考查等差数列的第4项和第10项的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
20.已知z1、z2均为复数,下列四个命题中,为真命题的是( )
| A. | |z1|=|$\overline{{z}_{1}}$|=$\sqrt{{{z}_{1}}^{2}}$ | |
| B. | 若|z2|=2,则z2的取值集合为{-2,2,-2i,2i}(i是虚数单位) | |
| C. | 若z12+z22=0,则z1=0或z2=0 | |
| D. | z1$\overline{{z}_{2}}$+$\overline{{z}_{1}}$z2一定是实数 |
17.下列函数既是奇函数又在(-1,1)上是增函数的是( )
| A. | y=cos($\frac{π}{2}$+x) | B. | y=-$\frac{2}{x}$ | C. | y=ln$\frac{2-x}{2+x}$ | D. | y=2x-2-x |
4.已知函数y=2x2,则自变量从2变到2+△x函数值的增量△y为( )
| A. | 8 | B. | 8+2△x | C. | 2(△x)2+8△x | D. | 4△x+2(△x)2 |
18.已知3a=2,2b=3,则a+b的取值范围为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
1.某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:
根据上表得回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,其中$\widehat{b}$=-3.2,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$,据此回归方程估计零售价为5元时销售量估计为( )
| x | 11 | 10.5 | 10 | 9.5 | 9 |
| y | 5 | 6 | 8 | 10 | 10 |
| A. | 16个 | B. | 20个 | C. | 24个 | D. | 28个 |
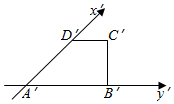 如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.
如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.