题目内容
20．已知z1、z2均为复数，下列四个命题中，为真命题的是（ ）| A． | |z1|=|$\overline{{z}_{1}}$|=$\sqrt{{{z}_{1}}^{2}}$ | |
| B． | 若|z2|=2，则z2的取值集合为{-2，2，-2i，2i}（i是虚数单位） | |
| C． | 若z12+z22=0，则z1=0或z2=0 | |
| D． | z1$\overline{{z}_{2}}$+$\overline{{z}_{1}}$z2一定是实数 |
分析 A．取z1=i，即可判断出正误；
B．由|z2|=2，则z2=2（cosθ+isinθ），θ∈[0，2π）；
C．取z1=i，z2=-i，即可否定；
D．设z1=a+bi，z2=c+di，a，b，c，d∈R，利用复数的运算法则即可判断出正误．
解答 解：A．不成立，例如取z1=i；
B．不成立，|z2|=2，则z2=2（cosθ+isinθ），θ∈[0，2π）；
C．不成立，例如取z1=i，z2=-i；
D．设z1=a+bi，z2=c+di，a，b，c，d∈R，则z1$\overline{{z}_{2}}$+$\overline{{z}_{1}}$z2=（a+bi）（c-di）+（a-bi）（c+di）=ac+bd+（bc-ad）i+ac-bd+（ad-bc）i=2ac，因此是实数，正确．
故选：D．
点评 本题考查了复数的运算法则及其有关知识，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
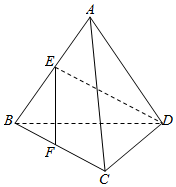如图，已知正三角形BCD外一点A满足AB=AD，E，F分别是AB，BC的中点，且EF⊥DE，则∠BAC=$\frac{π}{2}$．
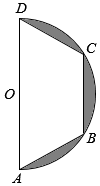如图，等腰梯形ABCD，BC=$\frac{1}{2}$AD，将直径为4的半圆内的阴影部分以直径AD所在直线为轴，旋转一周得到一几何体，求该几何体的体积．