题目内容
18.已知3a=2,2b=3,则a+b的取值范围为( )| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
分析 先根据对数式和指数式的互相转化,再分别判断a,b的范围,即可求出a+b的范围.
解答 解:∵3a=2,2b=3,
∴a=log32,b=log23,
∴a+b=log32+log23
∵$\frac{1}{2}$=log3$\sqrt{3}$<log32<log33=1,1=log22<log23<log24=2,
∴$\frac{3}{2}$<a+b<3,
∵a+b=log32+log23=a+b=log32+$\frac{1}{lo{g}_{3}2}$>2,
∴2<a+b<3,
故选:C.
点评 本题考查了对数函数的图象和性质以及基本不等式,属于基础题.

练习册系列答案
相关题目
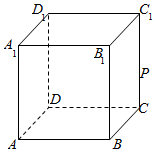 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.