题目内容
17．正弦函数f（x）=sinx图象的一条对称轴是（ ）| A． | x=0 | B． | $x=\frac{π}{4}$ | C． | $x=\frac{π}{2}$ | D． | x=π |
分析 根据三角函数的对称性进行求解即可．
解答 解：f（x）=sinx图象的一条对称轴为$x=\frac{π}{2}$+kπ，k∈Z，
∴当k=0时，函数的对称轴为$x=\frac{π}{2}$，
故选：C．
点评 本题主要考查三角函数的对称性，根据三角函数的对称轴是解决本题的关键．
练习册系列答案
相关题目
8．
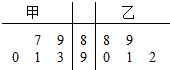甲、乙两名学生五次数学测验成绩（百分制）如图所示．
①甲同学成绩的中位数大于乙同学成绩的中位数；
②甲同学的平均分与乙同学的平均分相等；
③甲同学成绩的方差大于乙同学成绩的方差．
以上说法正确的是（ ）
甲、乙两名学生五次数学测验成绩（百分制）如图所示．①甲同学成绩的中位数大于乙同学成绩的中位数；
②甲同学的平均分与乙同学的平均分相等；
③甲同学成绩的方差大于乙同学成绩的方差．
以上说法正确的是（ ）
| A． | ①② | B． | ②③ | C． | ①③ | D． | ①②③ |
5．已知集合A={-1，0，1，2}，B={x|x＜2}，则A∩B=（ ）
| A． | {-1，0，1} | B． | {-1，0，2} | C． | {-1，0} | D． | {0，1} |
12．向顶角为120°的等腰三角形ABC（其中AC=BC）内任意投一点M，则AM小于AC的概率为（ ）
| A． | $\frac{{\sqrt{3}π}}{3}$ | B． | $\frac{{\sqrt{3}π}}{9}$ | C． | $\frac{1}{2}$ | D． | $\frac{π}{3}$ |
2．若函数f（x），g（x）分别是定义在R上的奇函数和偶函数，且满足f（x）+g（x）=ex，则下列结论正确的是（ ）
| A． | f（x）=$\frac{{e}^{x}-{e}^{-x}}{2}$且0＜f（1）＜g（2） | B． | f（x）=$\frac{{e}^{x}+{e}^{-x}}{2}$且0＜f（1）＜g（2） | ||
| C． | f（x）=$\frac{{e}^{x}-{e}^{-x}}{2}$且g（2）＜f（1）＜0 | D． | f（x）=$\frac{{e}^{x}+{e}^{-x}}{2}$且g（2）＜f（1）＜0 |
如图，在四边形ABCD中，AB=4，BC=$\frac{3}{2}$，CD=$\frac{5}{2}$，∠A=$\frac{π}{3}$，cos∠ADB=$\frac{1}{7}$．