题目内容
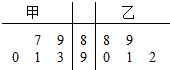
18. 已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1,x2分别表示知甲、乙两名同学这项测试成绩的众数,s12,s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( )
已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1,x2分别表示知甲、乙两名同学这项测试成绩的众数,s12,s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( )| A. | x1>x2,s12<s22 | B. | x1=x2,s12>s22 | C. | x1=x2,s12=s22 | D. | x1=x2,s12<s22 |
分析 根据茎叶图中的数据分别计算甲、乙运动员成绩的众数、平均数与方差,进行比较即可.
解答 解:根据茎叶图中的数据,得;
甲同学成绩的众数是x1=15,
平均数是$\overline{{x}_{1}}$=$\frac{1}{6}$(9+14+15+15+16+21)=15,
方差是${{s}_{1}}^{2}$=$\frac{1}{6}$[(9-15)2+(14-15)2+2×(15-15)2+(16-15)2+(21-15)2]=$\frac{37}{3}$;
乙运动员成绩的众数是x2=15,
平均数是$\overline{{x}_{2}}$=$\frac{1}{6}$(8+13+15+15+17+22)=15,
方差是${{s}_{2}}^{2}$=$\frac{1}{6}$[(8-15)2+(13-15)2+2×(15-15)2+(17-15)2+(22-15)2]=$\frac{53}{3}$;
∴x1=x2,${{s}_{1}}^{2}$<${{s}_{2}}^{2}$.
故选:D.
点评 本题利用茎叶图考查了求数据的众数、平均数与方差的应用问题,是基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8. 甲、乙两名学生五次数学测验成绩(百分制)如图所示.
甲、乙两名学生五次数学测验成绩(百分制)如图所示.
①甲同学成绩的中位数大于乙同学成绩的中位数;
②甲同学的平均分与乙同学的平均分相等;
③甲同学成绩的方差大于乙同学成绩的方差.
以上说法正确的是( )
 甲、乙两名学生五次数学测验成绩(百分制)如图所示.
甲、乙两名学生五次数学测验成绩(百分制)如图所示.①甲同学成绩的中位数大于乙同学成绩的中位数;
②甲同学的平均分与乙同学的平均分相等;
③甲同学成绩的方差大于乙同学成绩的方差.
以上说法正确的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
13.不等式组$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-y+1≥0}\\{2x+3y-4≤0}\end{array}\right.$,表示的平面区域绕着原点旋转一周所得到的平面图形的面积为( )
| A. | $\frac{12π}{25}$ | B. | $\frac{17π}{25}$ | C. | 3π | D. | $\frac{16π}{5}$ |
 如图,在四边形ABCD中,AB=4,BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=4,BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.