题目内容
(本小题满分14分)
(1) 证明:当 时,不等式
时,不等式 成立;
成立;
(2) 要使上述不等式 成立,能否将条件“
成立,能否将条件“ ”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;
”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;
(3)请你根据⑴、⑵的证明,试写出一个类似的更为一般的结论,且给予证明.
(1) 证明:当
 时,不等式
时,不等式 成立;
成立;(2) 要使上述不等式
 成立,能否将条件“
成立,能否将条件“ ”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;
”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;(3)请你根据⑴、⑵的证明,试写出一个类似的更为一般的结论,且给予证明.
(1)证明:见解析;
(2)∵ 对任何 且
且 ,式子
,式子 与
与 同号,恒成立,
同号,恒成立,
∴ 上述不等式的条件可放宽为 且
且 .
.
根据(1)(2)的证明,可推广为:若 且
且 ,
, ,
, ,
,
则有 .
.
证明:见解析。
(2)∵ 对任何
 且
且 ,式子
,式子 与
与 同号,恒成立,
同号,恒成立,∴ 上述不等式的条件可放宽为
 且
且 .
.根据(1)(2)的证明,可推广为:若
 且
且 ,
, ,
, ,
,则有
 .
.证明:见解析。
(1)证明易采用作差比较,然后对差值分解因式,再判断每个因式的符号,从而确定差值符号.
(2)根据(1)先观察成立时应具体什么条件,然后再采用作差比较法进行证明.
(1)证明:左式-右式=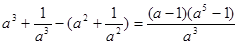 ,
,
∵ ,
,
∴
 ,
,
∴ 不等式 成立.
成立.
(2)∵ 对任何 且
且 ,式子
,式子 与
与 同号,恒成立,
同号,恒成立,
∴ 上述不等式的条件可放宽为 且
且 .
.
根据(1)(2)的证明,可推广为:若 且
且 ,
, ,
, ,
,
则有 .
.
证明:左式-右式
 .
.
若 ,则由
,则由 不等式成立;
不等式成立;
若 ,则由
,则由 不等式成立.
不等式成立.
∴ 综上得: 若 且
且 ,
, ,
, ,
,
则有 成立.
成立.
注:(3)中结论为:若 且
且 ,
, ,
,
则有 也对.
也对.
(2)根据(1)先观察成立时应具体什么条件,然后再采用作差比较法进行证明.
(1)证明:左式-右式=
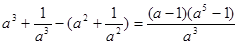 ,
,∵
 ,
, ∴

 ,
,∴ 不等式
 成立.
成立.(2)∵ 对任何
 且
且 ,式子
,式子 与
与 同号,恒成立,
同号,恒成立,∴ 上述不等式的条件可放宽为
 且
且 .
.根据(1)(2)的证明,可推广为:若
 且
且 ,
, ,
, ,
,则有
 .
.证明:左式-右式

 .
.若
 ,则由
,则由 不等式成立;
不等式成立;若
 ,则由
,则由 不等式成立.
不等式成立.∴ 综上得: 若
 且
且 ,
, ,
, ,
,则有
 成立.
成立.注:(3)中结论为:若
 且
且 ,
, ,
,则有
 也对.
也对.
练习册系列答案
相关题目
 >
> ,x>y.
,x>y.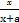 >
>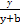 .
.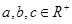 ,求证:
,求证: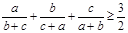 .
.

 ≥8.
≥8. ,且
,且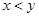 ,求证:
,求证:
 ,判断
,判断 与
与 的大小,并证明你的结论.
的大小,并证明你的结论. ,对任意正数
,对任意正数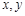 ,
, 始终可以是一个三角形的三条边,则实数m的取值范围为 .
始终可以是一个三角形的三条边,则实数m的取值范围为 . 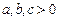 ,求证:
,求证: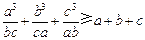 .
.