题目内容
(本小题满分12分)
设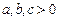 ,求证:
,求证: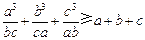 .
.
设
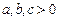 ,求证:
,求证: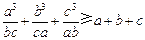 .
.略
证:由对称性,不妨设 ,则
,则 ,
, ,得
,得 ,由排序不等式,得顺序和
,由排序不等式,得顺序和 乱序和,则
乱序和,则 即
即 又
又
 又由乱序和
又由乱序和 逆序和,则
逆序和,则 ,即
,即 ,所以
,所以
 ,则
,则 ,
, ,得
,得 ,由排序不等式,得顺序和
,由排序不等式,得顺序和 乱序和,则
乱序和,则 即
即 又
又
 又由乱序和
又由乱序和 逆序和,则
逆序和,则 ,即
,即 ,所以
,所以

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
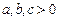 ,求证:
,求证: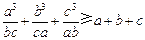 .
. ,则
,则 ,
, ,得
,得 ,由排序不等式,得顺序和
,由排序不等式,得顺序和 乱序和,则
乱序和,则 即
即 又
又
 又由乱序和
又由乱序和 逆序和,则
逆序和,则 ,即
,即 ,所以
,所以

 阅读快车系列答案
阅读快车系列答案