题目内容
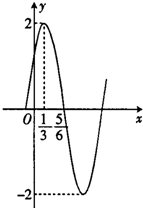 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
(1)试确定函数f(x)的解析式.
(2)若f(
| α |
| 2π |
| 1 |
| 3 |
| π |
| 3 |
| α |
| 2 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:(1)由已知得A=
=2,w=
=
=π,由此结合图象能求出f(x).
(2)由已知得sin(
-
)=
,由此能求出cos(
-
).
| 2-(-2) |
| 2 |
| 2π |
| T |
| 2π | ||||
4(
|
(2)由已知得sin(
| α |
| 2 |
| π |
| 3 |
| 1 |
| 6 |
| π |
| 3 |
| α |
| 2 |
解答:
解:(1)由已知得A=
=2,
w=
=
=π,
∴f(x)=2sin(πx+φ),
把(
,2)代入,得2=2sin(
π+φ),
∵|φ|<
,∴结合图象得φ=-
,
∴f(x)=2sin(πx-
).
(2)∵f(
)=
,
∴2sin(
-
)=
,即sin(
-
)=
,
∴cos(
-
)=cos(
-
)=±
=±
.
| 2-(-2) |
| 2 |
w=
| 2π |
| T |
| 2π | ||||
4(
|
∴f(x)=2sin(πx+φ),
把(
| 1 |
| 3 |
| 1 |
| 3 |
∵|φ|<
| π |
| 2 |
| π |
| 3 |
∴f(x)=2sin(πx-
| π |
| 3 |
(2)∵f(
| α |
| 2π |
| 1 |
| 3 |
∴2sin(
| α |
| 2 |
| π |
| 3 |
| 1 |
| 3 |
| α |
| 2 |
| π |
| 3 |
| 1 |
| 6 |
∴cos(
| π |
| 3 |
| α |
| 2 |
| α |
| 2 |
| π |
| 3 |
1-(
|
| ||
| 6 |
点评:本题考查三角函数的解析式的求法,考查三角函数值的求法,是基础题,解题时要认真审题,注意三角函数的性质的合理运用.

练习册系列答案
相关题目
已知x,y是两个具有线性相关关系的变量,现有这两个变量的十个样本点(x1,y1)(x2,y2),…,(x10,y10),同学甲利用最小二乘法得到回归直线l1:y=bx+a,同学乙将十个样本点中的两个点连起来得到拟合直线l2:y=dx+c,则下列判断一定正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
同时抛掷三枚均匀的硬币,均为正面向上的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
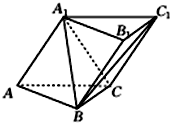 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC.
 已知直线l1:y=
已知直线l1:y=