题目内容
求函数y=
-sin
cos
的导数.
| ex |
| x |
| 2 |
| x |
| 2 |
考点:导数的运算
专题:导数的概念及应用
分析:利用函数求导公式解答.
解答:
解:y=
-sin
cos
=
-
sinx=e
-
sinx,
所以y′=(e
-
sinx)′=
ex2-
cosx.
| ex |
| x |
| 2 |
| x |
| 2 |
| ex |
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
所以y′=(e
| x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了二倍角公式以及函数求导,属于基础题.

练习册系列答案
相关题目
若等比数列{an}的前n项和为Sn,且S3=14,a1=2,则a4=( )
| A、16 | B、16或-16 |
| C、-54 | D、16或-54 |




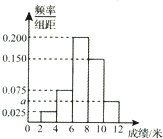 为了解某市今年八年级生的身体状况,从中抽取了一部份学生进行掷铅球的项目测试,成绩低于6米的为不合格,成绩在6至8米的(含6米不含8米)为及格,成绩在8至12米(含8米不含12米)为优秀.假定每个学生成绩均不超过12米.画出频率分布图如图.已知有4名学生的成绩在10米至12米之间.
为了解某市今年八年级生的身体状况,从中抽取了一部份学生进行掷铅球的项目测试,成绩低于6米的为不合格,成绩在6至8米的(含6米不含8米)为及格,成绩在8至12米(含8米不含12米)为优秀.假定每个学生成绩均不超过12米.画出频率分布图如图.已知有4名学生的成绩在10米至12米之间.