题目内容
平行四边形ABCD中，O是两条对角线AC，BD的交点，设点集S={A，B，C，D，O}，向量集合T={
|，M，N∈S且M、N不重合}，试求集合T的子集的个数．
| MN |
考点：子集与真子集
专题：集合
分析：首先求出满足条件的所有向量，然后利用集合子集的求法解答．
解答：
解：根据向量的特点，向量集合T={
|，M，N∈S且M、N不重合}，满足条件的向量有
-8=12，
所以点集S的元素个数为12个，子集有212个；
| MN |
| A | 2 5 |
所以点集S的元素个数为12个，子集有212个；
点评：本题考查向量的性质以及集合子集是求法．
练习册系列答案
相关题目
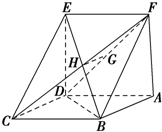如图，已知平行四边形ABCD中，BC=2，BD⊥CD，四边形ADEF为正方形，平面ADEF⊥平面ABCD，G，H分别是DF，BE的中点．四棱锥F-ABCD的体积的最大值（ ）| A、4 | ||
B、
| ||
C、
| ||
| D、2 |
已知f（x）=x3+2x，则f（5）+f（-5）的值是（ ）
| A、0 | B、-1 | C、1 | D、2 |
已知函数f（x）=Asin（ωx+φ） （x∈R，A＞0，ω＞0，|φ|＜