题目内容
已知数列{an}的前n项和为Sn,且Sn=
n2+
n.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,b1+b2+…+b9=153.
(1)求数列{an},{bn}的通项公式;
(2)设cn=
,数列{cn}的前n项和为Tn,求使不等式Tn>
对一切n∈N*都成立的最大正整数k的值.
| 1 |
| 2 |
| 11 |
| 2 |
(1)求数列{an},{bn}的通项公式;
(2)设cn=
| 3 |
| (2an-11)(2bn-1) |
| k |
| 57 |
考点:数列与不等式的综合,数列的求和,数列递推式
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:(1)通过n=1,求出a1,当n≥2时,利用an=Sn-Sn-1,求出an=n+5(n≥2),通过bn+2-2bn+1+bn=0推出{bn}是等差数列,求出bn.
(2)利用cn=
,通过裂项法化简,求出Tn,判断Tn单调递增,推出(Tn)min=T1=
,得到
>
,求出kmax即可.
(2)利用cn=
| 3 |
| (2an-11)(2bn-1) |
| 1 |
| 3 |
| 1 |
| 3 |
| k |
| 57 |
解答:
解:(1)当n=1时,a1=S1=6
当n≥2时,an=Sn-Sn-1=(
n2+
n)-[
(n-1)2+
(n-1)]=n+5,
∴an=n+5(n≥2)
又a1=6也适合上式∴a n=n+5(n∈N+)
又bn+2-2bn+1+bn=0即bn+2-bn+1=bn+1-bn,
所以{bn}是等差数列,又b3=11,b1+b2+…+b9=153,解得b1=5,d=3.
因为bn=3n+2…(6分)
(2)cn=
=
=
(
-
)
所以Tn=c1+c2+…cn=
[(1-
)+(
-
)+…+(
-
)]=
…(8分)
因为Tn+1-Tn=
-
=
>0…(10分)
因为Tn单调递增,故(Tn)min=T1=
…(11分)
令
>
,得k<19,所以kmax=18.…(13分)
当n≥2时,an=Sn-Sn-1=(
| 1 |
| 2 |
| 11 |
| 2 |
| 1 |
| 2 |
| 11 |
| 2 |
∴an=n+5(n≥2)
又a1=6也适合上式∴a n=n+5(n∈N+)
又bn+2-2bn+1+bn=0即bn+2-bn+1=bn+1-bn,
所以{bn}是等差数列,又b3=11,b1+b2+…+b9=153,解得b1=5,d=3.
因为bn=3n+2…(6分)
(2)cn=
| 3 |
| (2an-11)(2bn-1) |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
所以Tn=c1+c2+…cn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
因为Tn+1-Tn=
| n+1 |
| 2n+3 |
| n |
| 2n+1 |
| 1 |
| (2n+3)(2n+1) |
因为Tn单调递增,故(Tn)min=T1=
| 1 |
| 3 |
令
| 1 |
| 3 |
| k |
| 57 |
点评:本题考查数列的综合应用,数列求和,递推关系式以及通项公式的求法,数列的单调性以及不等式的应用,考查分析问题解决问题以及转化思想的应用.

练习册系列答案
相关题目
已知二项式(
-
)7展开式的第4项与第5项之和为零,那么x等于( )
| x |
| 2 | ||
|
| A、1 | ||
B、
| ||
| C、2 | ||
| D、46 |
设函数f1(x)=log4x-(
)x、f2(x)=log
x-(
)x的零点分别为x1、x2,则( )
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| A、x1x2≥2 |
| B、1<x1x2<2 |
| C、x1x2=1 |
| D、0<x1x2<1 |
某几何体的三视图如图所示,它的体积为( )
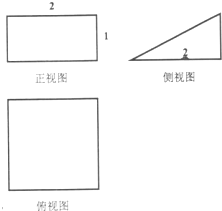

| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
 如图,有一块边长为1km的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45° (其中点P,Q分别在边BC,CD上),设∠PAB=θ,tanθ=t
如图,有一块边长为1km的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45° (其中点P,Q分别在边BC,CD上),设∠PAB=θ,tanθ=t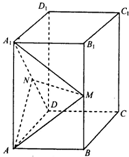 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.