题目内容
19.已知△ABC的内角A,B,C的对边分别为a,b,c,若$\sqrt{3}$acosC+($\sqrt{3}$c-2b)cosA=0,且cosA•cosC=$\frac{\sqrt{3}}{4}$,则△ABC是( )| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等边三角形 | D. | 等腰三角形或直角三角形 |
分析 利用正弦定理化简已知等式可得$\sqrt{3}$sinAcosC+$\sqrt{3}$sinCcosA=2sinBcosA,由诱导公式及三角形内角和定理可得$\sqrt{3}$sinB=2sinBcosA,结合范围B∈(0,π),sinB>0,可求A,又cosA•cosC=$\frac{\sqrt{3}}{4}$,解得cosC=$\frac{1}{2}$,由范围C∈(0,π),可求C,从而求得B=$\frac{π}{2}$,即可得解.
解答 解:∵$\sqrt{3}$acosC+($\sqrt{3}$c-2b)cosA=0,
∴由正弦定理可得:$\sqrt{3}$sinAcosC+$\sqrt{3}$sinCcosA=2sinBcosA,
∴$\sqrt{3}$sin(A+C)=$\sqrt{3}$sinB=2sinBcosA,
∵B∈(0,π),sinB>0,
∴解得:cosA=$\frac{\sqrt{3}}{2}$,由A∈(0,π),可得:A=$\frac{π}{6}$,
又∵cosA•cosC=$\frac{\sqrt{3}}{4}$,解得:cosC=$\frac{1}{2}$,
∴由C∈(0,π),可得:C=$\frac{π}{3}$,
∴B=π-A-C=$\frac{π}{2}$.
故选:A.
点评 本题主要考查了正弦定理,三角形内角和定理,诱导公式,两角和的正弦函数公式,余弦函数的图象和性质的应用,属于中档题.

练习册系列答案
相关题目
10.在区间[0,2π]上随机取一个数x,则事件“cosx≥$\frac{1}{2}$”发生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{11}{12}$ |
7.若存在a∈R,使关于x的不等式x|x-a|<m+1在(0,1]上恒成立,则实数m的取值范围为( )
| A. | (2-2$\sqrt{2}$,2+2$\sqrt{2}$) | B. | (-1,+∞) | C. | (2-2$\sqrt{2}$,+∞) | D. | (-1,2+2$\sqrt{2}$) |
4.已知直线l经过点P(0,0),Q(-1,$\sqrt{3}$),则直线l的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
11.有两件事和四个图象,两件事为:①我离开家不久,发现自己把作业本忘在家里了,于是返回家找到作业本再上学;②我出发后,心情轻松,缓缓前行,后来为了赶时间开始加速,四个图象如下:
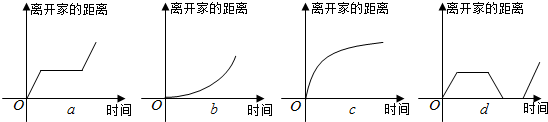
与事件①,②对应的图象分别为( )

与事件①,②对应的图象分别为( )
| A. | a,b | B. | a,c | C. | d,b | D. | d,c |
8.质点沿直线运动的路程和时间的关系是s=$\root{5}{t}$.则质点在t=4时的速度是( )
| A. | $\frac{1}{2\root{5}{{2}^{3}}}$ | B. | $\frac{1}{10\root{5}{{2}^{3}}}$ | C. | $\frac{1}{\frac{2}{5}\root{5}{{2}^{3}}}$ | D. | $\frac{1}{\frac{1}{10}\root{5}{{2}^{3}}}$ |
9.sin22°30′•cos22°30′的值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |